PGM 复习

去年上了古槿老师的概率图的课，受益匪浅，但是过了大半年没有接触又忘了许多，所以打算重新复习一番，希望能有新的体悟。

PGM 中的结构，画出来感觉结构会清晰很多

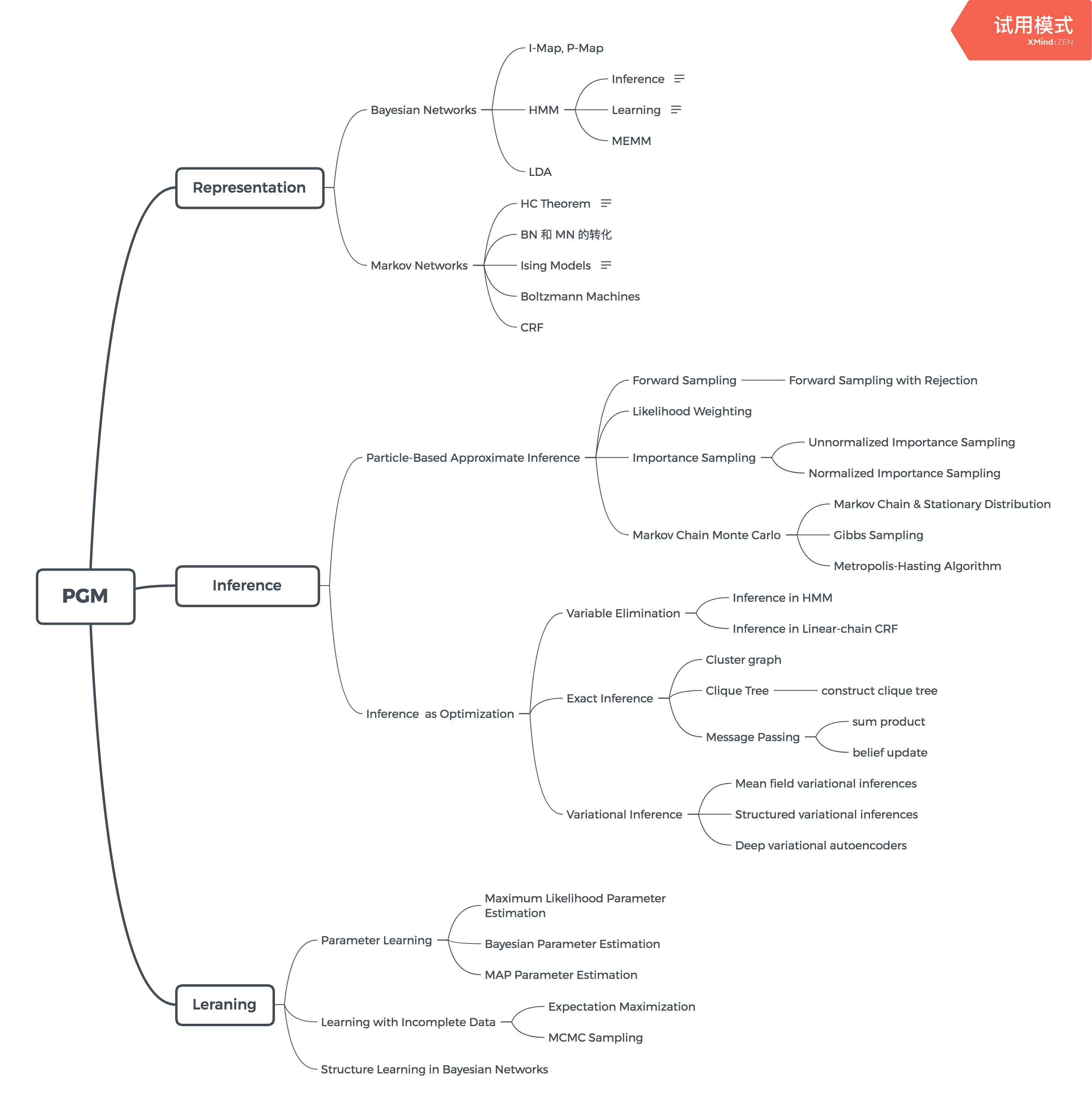
Introduction to PGM

Probability: decision making based on probability

如果有n个因素会影响最后的决策，那么参数的个数会呈指数型的增长，如果因素是二值的，那么会有 $2^n$ 个参数，但如果是用一个graph来表示n个因素的关系，将会大大减少参数量，这也是为什么概率图产生的原因吧

Probability 的基础：

1. Frequentist probability：$p(x)\approx \frac{n_x}{n_t}$ $p(x)=\lim_{n_t \to \infty}\frac{n_x}{n_t}$
2. Bayesian probability: 定义一些先验概率，就能计算一些后验概率
3. 相关名词：random variable，joint probability，marginal probability，conditional probability，probability function，probability density function，independence，conditional independence
4. Chain rule：$p(X_1, X_2, …, X_n)=P(X_1)P(X_2\|X_1)…P(X_n\|X_1, …, X_{n-1})$
5. 全概率公式：$P(X)=\sum_Y P(XY)=\sum_Y P(X\|Y) P(Y)$
6. Bayes’ theorem: $P(X\|Y)=\frac{P(X, Y)}{P(Y)}=\frac{P(Y\|X)P(X)}{P(Y)}=\frac{P(Y\|X)P(X)}{\sum_X P(Y\|X)P(X)}$

Graph 的基础

1. G(V, E): node/vertex, edges
2. path, trail, connectivity
3. Polytree, tree, chordal graph
4. Centrality: degree, betweenness, closeness
5. Subgraph, cut, clique

PGM的应用场景

这几个也是面试时候会问的，毕竟日常场景使用会比较多

1. HMM：股票市场指数
2. VAE：Dimension Reduction
3. CRF: 图像分割，后面章节其实提到了是Ising model，但没有想到是用来作图像分割的

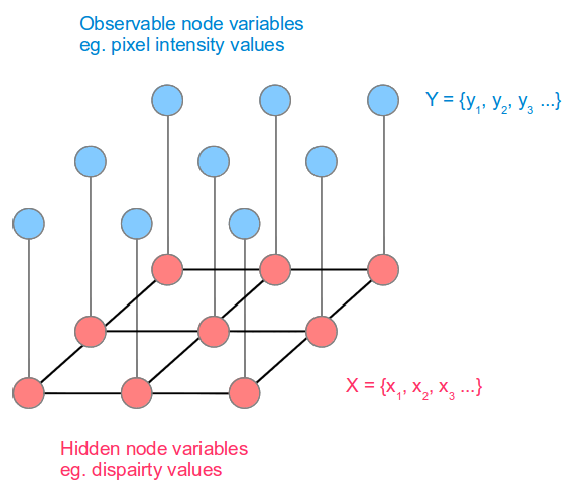
隐变量和它临近节点是有相似值，因为图像在同一块区域一般不会有突变

1. CNN：计算机视觉，举这个例子感觉和PGM不是很扯的上边

古老师分了十一个章节来阐述PGM，而且特别注重Representation，当时上课感觉这个层层递进，老师讲的也特别清楚，希望一章一章能逐步复习完，加油！

• Representation
  • Chap1 Introduction
  • Chap2 Bayesian Network
  • Chap3 Local Probabilistic Model
  • Chap4 Dynamic Bayesian Networks
  • Chap5 Markov Random Fields
  • Chap6 Advanced Models
• Inference
  • Chap7 Variational Inference
  • Chap8 Particle Based Approximate Inference
  • Chap9 MAP Inference
• Learning
  • Chap10 Bayesian Netowrk Learning
  • Chap11 Learning with Incomplete Data

Naive Bayesian Model

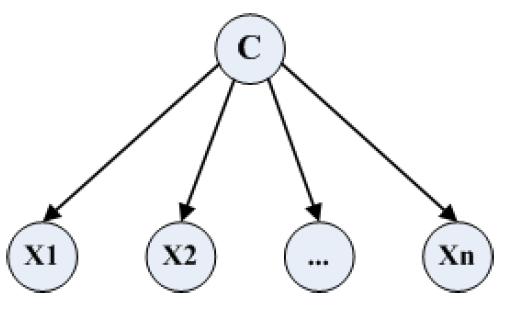
如果类标签给定了，那所有的观测变量都是独立的

$$P(X_1, X_2, X_3, C) = P(X_1\|C)P(X_2\|C)P(X_3\|C)P(C)$$

Representation: $P\Leftrightarrow \{P, G/H\}$ 其中G代表有向图，H代表无向图

Inference： $P(C\|X=x, \theta)$

Learning: $P(\theta \| x^1, x^2, ...)$