LDA 主题模型——Latent Dirichlet Allocation

LDA（Latent Dirichlet Allocation）是一种文档主题生成模型（generative model），也称为一个三层贝叶斯概率模型，包含词、主题和文档三层结构。

文档到主题服从多项式分布，主题到词服从多项式分布。Dirichlet Distribution 是多项式分布的共轭先验分布。

LDA是一种非监督机器学习技术，可以用来识别大规模文档集或语料库中潜藏的主题信息。

它采用了词袋（bag of words）的方法，这种方法将每一篇文档视为一个词频向量，从而将文本信息转化为了易于建模的数字信息。但是词袋方法没有考虑词与词之间的顺序。

每一篇文档代表了一些主题所构成的一个概率分布，而每一个主题又代表了很多单词所构成的一个概率分布。

对于语料库中的每篇文档，LDA定义了如下生成过程（generative process）：

1. 按照概率$P(d_i)$选中一篇文档$d_i$
2. 从Dirichlet分布$\alpha$ 中抽样生成文档 $d_i$ 的主题分布$\theta_m$
3. 从主题分布 $\theta_m$ 中抽取文档 $d_i$ 第 j 个词的主题 $z_{m,n}$
4. 从Dirichlet分布 $\beta$ 中抽样生成主题 $z_{m,m}$ 对应的词分布 $\varphi_k$
5. 从词分布 $\varphi_k$ 中抽样生成词 $w_{m,n}$

每一篇文档与 T 个主题的一个多项分布 （multinomial distribution）相对应，将该多项分布记为θ。

每个主题又与词汇表（vocabulary）中的 V 个单词的一个多项分布相对应，将这个多项分布记为φ。

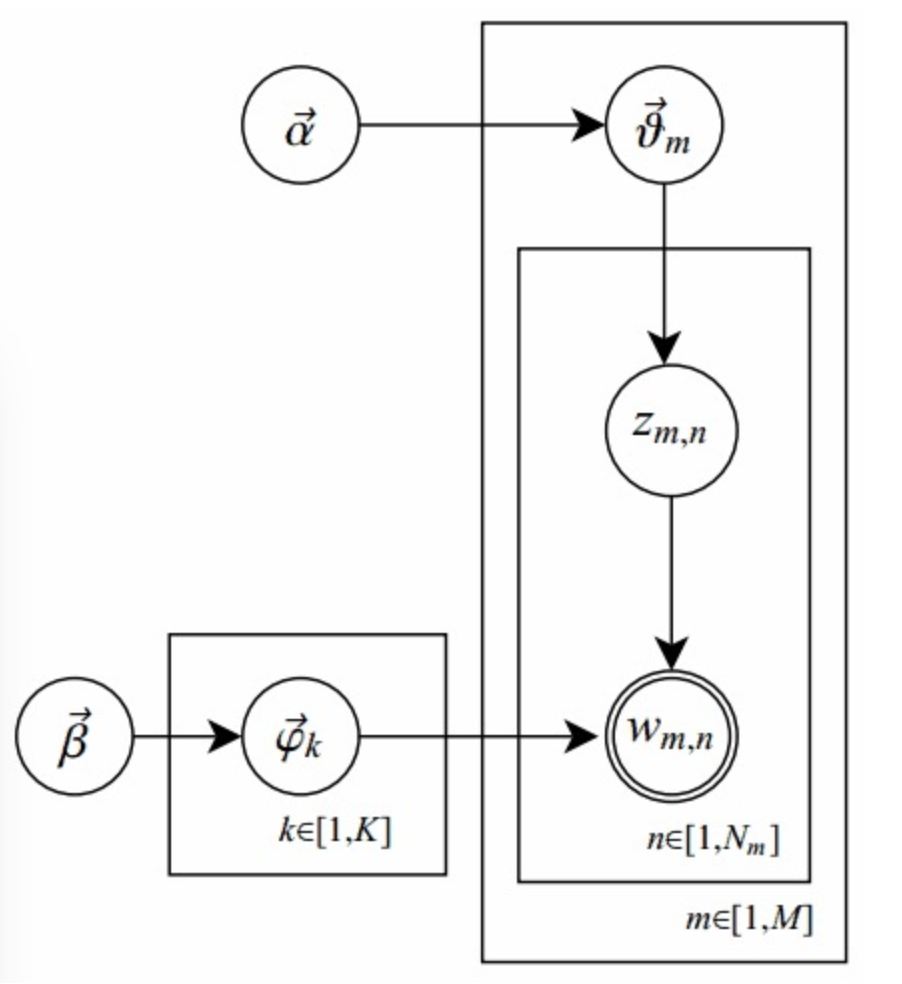
先定义一些字母的含义：

• 文档集合 D

• 主题（topic) 集合 T

• D 中每个文档 d 看作一个单词序列 <w1, w2, …, wn>，wi 表示第 i 个单词，设 d 有 n 个单词。（LDA 里面称之为word bag，实际上每个单词的出现位置对 LDA 算法无影响）

• D中涉及的所有不同单词组成一个大集合 VOCABULARY（简称 VOC），LDA 以文档集合 D 作为输入，希望训练出的两个结果向量（设聚成 k 个topic，VOC 中共包含 m 个词）：
  • 对每个 D 中的文档 d，对应到不同 Topic 的概率 $θ_d<p_{t_1},…,p_{t_k}>$，其中，$p_{t_i}$表示 d 对应 T 中第 i 个 topic 的概率。计算方法是直观的，$p_{t_i}=\frac{n_{t_i}}{n}$，其中 $n_{t_i}$表示 d 中对应第 i 个 topic 的词的数目，n 是 d 中所有词的总数。
  • 对每个 T 中的 topic t，生成不同单词的概率 $\phi_t <p_{w_1},…,p_{w_m}>$ ，其中，$p_{w_i}$表示 t 生成 VOC 中第 i 个单词的概率。计算方法同样很直观，$p_{w_i}=\frac{N_{w_i}}{N}$ ，其中$N_{w_i}$表示对应到 topic t 的 VOC 中第 i 个单词的数目，N 表示所有对应到 topic t 的单词总数。

LDA的核心公式如下：$p(w\|d)=p(w\|t)*p(t\|d)$

直观的看这个公式，就是以Topic作为中间层，可以通过当前的 $θ_d$ 和 $φ_t$ 给出了文档 d 中出现单词 w 的概率。其中p(t|d)利用 $θ_d$ 计算得到，p(w|t) 利用 $φ_t$ 计算得到。

实际上，利用当前的 $θ_d$ 和 $φ_t$，我们可以为一个文档中的一个单词计算它对应任意一个 Topic 时的 p(w|d)，然后根据这些结果来更新这个词应该对应的 topic。然后，如果这个更新改变了这个单词所对应的 Topic，就会反过来影响 $θ_d$ 和 $φ_t$。

LDA算法开始时，先随机地给 $θ_d$ 和 $φ_t$ 赋值(对所有的 d 和 t )。然后上述过程不断重复，最终收敛到的结果就是LDA的输出。

再详细说一下这个迭代的学习过程：

1. 针对一个特定的文档 $d_s$ 中的第 i 单词 $w_i$，如果令该单词对应的 topic 为 $t_j$，可以把上述公式改写为：$p_j(w_i\|d_s)=p(w_i\|t_j)*p(t_j\|d_s)$

2. 现在我们可以枚举 T 中的 topic j，得到所有的$p_j(w_i\|d_s)$，其中 j 取值 1~k。然后可以根据这些概率值结果为 $d_s$中的第 i 个单词 $w_i$ 选择一个topic。最简单的想法是取令 $p_j(w_i\|d_s)$ 最大的 $t_j$（注意，这个式子里只有j是变量），即$\arg\max_j p_j(w_i\|d_s)$

3. 然后，如果 $d_s$中的第 i 个单词 $w_i$ 在这里选择了一个与原先不同的topic，就会对 $θ_d$ 和 $φ_t$有影响了（根据前面提到过的这两个向量的计算公式可以很容易知道）。它们的影响又会反过来影响对上面提到的 p(w|d) 的计算。对D中所有的d中的所有w进行一次 p(w|d) 的计算并重新选择topic 看作一次迭代。这样进行n次循环迭代之后，就会收敛到LDA所需要的结果了。

PLSI 可以依赖 EM 算法得到较好的解决，LDA 的学习属于 Bayesian Inference，只有 MCMC 或者 Variational Inference 可以解决。LDA 原始论文使用的 VI 来解决，但是后续大多数 LDA 相关论文都选择了 MCMC 为主的 Gibbs Sampling 来作为学习算法。

从最高的层次上来理解，VI 是选取一整组简单的、可以优化的变分分布（Variational Distribution）来逼近整个模型的后验概率分布。当然，由于这组分布的选取，有可能会为模型带来不小的误差。不过好处则是这样就把Bayesian Inference的问题转化成了optimization问题。

从 LDA 的角度来讲，就是要为θ以及 z 选取一组等价的分布，只不过更加简单，更不依赖其他的信息。在 VI 进行更新 θ 以及 z 的时候，算法可以根据当前的 θ 以及 z 的最新值，更新 $\alpha$ 的值（这里的讨论依照原始的 LDA 论文，忽略了β的信息）。整个流程俗称变分最大期望（Variational EM）算法。

Basic Related Math

Gamma Function

这是个函数！不是分布！

$$\Gamma(x)=\int_0^\infty t^{x-1} e^{-t} dt$$

Gamma 函数有个很好的递归性质：$\Gamma(x+1)=x\Gamma(x)$

可以表述为阶乘在实数集上的延展：$\Gamma(n)=(n-1)!$

Binomial Distribution

二项分布，伯努利分布(0-1 分布)：$P(K=k)=\dbinom{n}{k} p^k (1-p)^{n-k}$

Multinomial Distribution

多项式分布：$P(x_1, …, x_k;n,p_1, …, p_k)=\frac{n!}{x_1!…x_k!}p_1^{x_1}…p_k^{x_k}$

Beta Distribution

$\theta \sim Beta (\alpha_1, \alpha_0)$ if $P(\theta)=\gamma \theta^{\alpha_1-1}(1-\theta)^{\alpha_0-1}$

$\gamma=\frac{\Gamma(\alpha_1+\alpha_0)}{\Gamma(\alpha_1)\Gamma(\alpha_0)}$ Is a normalizing factor

$$\Gamma(x)=\int_0^\infty t^{x-1}e^{-t}\, dt$$

有非常好的Beta-Binomial共轭性质，因为 beta 分布的形式和二项分布的形式相似，由符合 beta 分布的参数先验推出的后验分布也符合 beta 分布(共轭分布的性质)。例如：二项分布的先验分布服从beta 分布 $\theta \sim Beta (\alpha_1, \alpha_0)$ ，已知投了 5 次硬币，3 次 X=1，2 次 X=0，那么新的预测分布更新为 $P(x[m+1]\|X)=Beta(\alpha_1+3, \alpha_0+2)$

Beta-Binomial 共轭意味着，如果为二项分布的参数θ选取的先验分布是Beta分布，那么以θ为参数的二项分布用贝叶斯估计得到的后验分布P(θ|X)仍然服从Beta分布，那么Beta分布就是二项分布的共轭先验分布

$$Beta(\alpha_1, \alpha_0)+BinorCount(m_1, m_0)=Beta(\alpha_1+m_1, \alpha_0+m_0)$$

采用共轭先验的原因：

可以使得先验分布和后验分布的形式相同，这样一方面合符人的直观（它们应该是相同形式的）另外一方面是可以形成一个先验链，即现在的后验分布可以作为下一次计算的先验分布，如果形式相同，就可以形成一个链条。

后验概率 ∝ 似然函数*先验概率 即 $P(\theta\|X)\propto P(X\|\theta) P(\theta)$

另外，θ的期望：$E(\theta)=\frac{\alpha_1}{\alpha_1+\alpha_0}$

Dirichlet Distribution

dirichlet 分布式 Beta 分布的推广：

$$\theta \sim Dirichlet(\alpha_1, …, \alpha_k)=\gamma \prod_{i=1}^k \theta_i^{\alpha_i-1}$$ $$\gamma=\frac{\Gamma({\sum_{i=1}^k \alpha_i})}{\prod_{i=1}^k \Gamma(\alpha_i)}$$ $$\sum_{i=1}^k \theta_i = 1$$ $$Dirichlet(\vec{\alpha}) + MultiCount(\vec{m})=Dirichlet(\vec{\alpha}+\vec{m})$$

Dirichlet 分布的期望：$E(\theta) = (\frac{\alpha_1}{\sum_{i=1}^K \alpha_i}, …, \frac{\alpha_K}{\sum_{i=1}^K \alpha_i})$