Structure Variational Inference 是在 PGM 经常使用的推断方法!
Variational Inference的基本思想和 Importance Sampling 有点像(从分布 Q 中采样来模拟从 P 中采样的样本):为了推断目标 P(X), 找到另一个分布 Q(X)来近似,这样就可以在 Q(X) 上更容易做 inference。因为有的时候 P(X)很复杂无法exactly 求出来,可以用分布 Q(X) 近似 P(X),可能不是完全细节一致,但是大体是一致(这也是为什么后面用 Variational Inference 来做 autoencoder,可以去掉一些噪声),分布 Q(X)比 P(X)简单。
本章只讨论有向图 G 上的变分推断
Variational inference is an optimization process to find a variational distribution Q(X) from a distribution family by maximizing an energy functional
P(X):target distribution
Q(X): variational/proposal distribution,Q 是由比 P更简单形式构成的分布族,如高斯分布族,所以可以用来 de-noising 或者 dimension reduction
KL divergence:是衡量两个分布距离的测量标准
Or
Q 在前面,对 Q 做期望,有负号是为了凑熵的形式
目标:
找到和分布P KL 距离最小的分布 Q,其实只要是测量分布距离的标准都可以,目标就是尽量使 Q 在这个标准下靠近 P
Structured variational inference
Q(X):定义在简单结构G上的分布,比如没有边的图(mean field algorithm), G 上都是相互独立的节点
假设 Q(X)是高斯分布族:
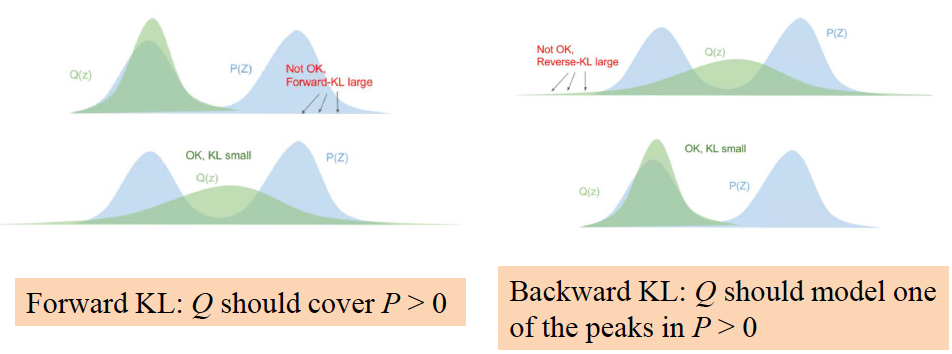
- Forward KL(M-projection):, Q 需要 cover P 的全部范围
- Backward KL(I-projection): 一般都使用 backward KL,Q 只需要 model P 的一个 peak 就行
Energy Functional
令 target distribution P(X|Z=z),那么 KL 距离:
<— Energy functional
Q1: 如何选择Q(X)分布的分布族?
Q2:如何最大化 energy functional?
原始目标
energy functional 第一项 ,是用来近似 P 的,P 和 Q 越像,第一项的值就越大
energy functional 第二项 ,是用来防止过拟合的,让 Q(X)四散,尽量 cover 更多范围,防止拟合到
Evidence Lower Bound(ELBO)
因为 KL 距离是非负的,所以 energy functional 的 bound 是 ln P(z)
L(Q) 也叫 ELBO
Mean Field Variational Inference
目标:推断(计算)p(x|z)——很难直接计算
使用简单的分布 q 来模拟分布 p,这个简单的分布 q 就是完全分解的形式
打公式好累。。。直接上图吧。。。

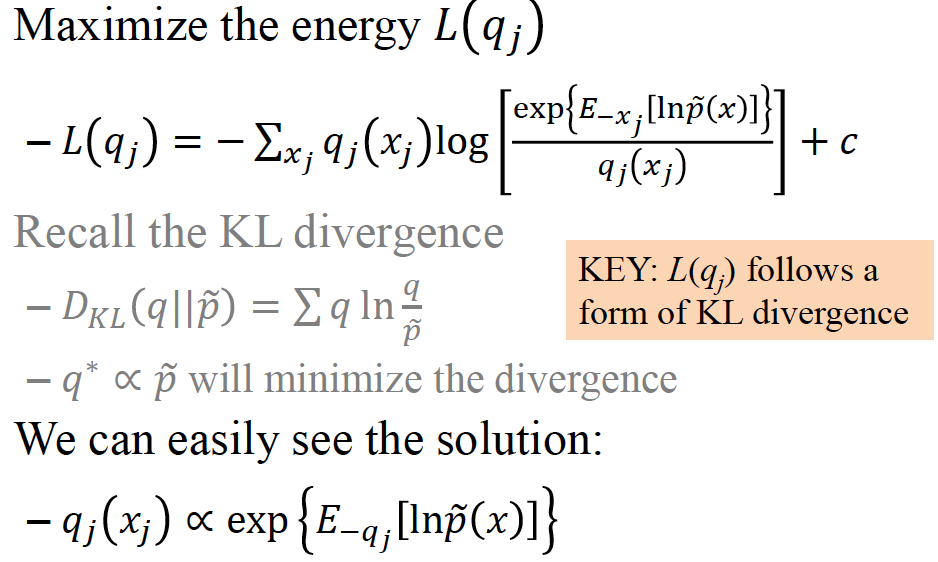
L(q),ELBO 的形式和 KL 距离的形式一致,由 KL 距离得知,当 q 和 p 的分布越接近,kl 距离越小。
同理,和 成正比能够求得L(q_j)的最大值。




总结一下structure variational inference:
- KL 距离
- 由 KL 距离,推出 energy functional L(q)。且最小化 KL 距离等于最大化 energy functional
- 由和 KL 距离公式形式一样,推出最优解使得最优值正比于
- 所以如果要求出分布,求就行
- 由图求出
- 设 的 分布族(the family of the variational distribution)
- 代入 1,2 得到,即得到
- 得到最优参数
- 迭代求得每个参数
- 得到 后就从 q*做 inference ,而不是 p 了,因为此时 q *已经近似了 p
LDA 中的变分推断,需要特别开一章进行学习。
注意,变分推断中,近似的 q ,变量 variables 需要和 p 相同,参数可不同
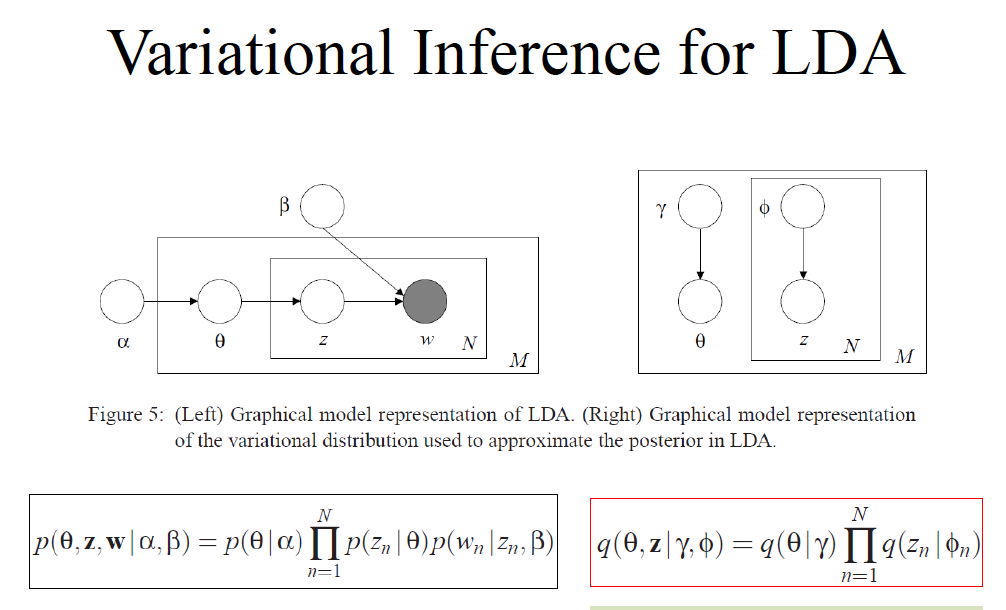
变量都是,但是参数是和
在很多情况下,无法用平均场的变分推断求出近似解,此时随机梯度下降的方法是经常使用到的。

Variational inference can be regarded as a kind of learning: find the optimal parameters by maximizing an energy functional
Learning as MLE: find the optimal parameters by maximizing likelihood function given data.