Chap4 Dynamic Bayesian Networks

HMM 是 generative model，生成式模型。HMM 有两种 inference 问题，和一个 learning 问题。

Inference 1：$P(X\|\theta)$ ，已知模型$\theta$和观察序列$X$，推测该模型得到该观测序列的概率。基本的想法是由联合分布 $P(X, Y\|\theta)$, 积掉 Y，得到$P(X\|\theta)$。$P(X, Y\|\theta)$ 用分解定理分解为由$P(Y_{i-1}\|Y_i), P(X_i\|Y_i)$项组成的连乘公式。积掉$P(X, Y\|\theta)$ 可以从两个方向积，一个是从前往后积(Forward)，一个是从后往前积(Backward)，所以有了 Forward/Backward Algorithm

Inference 2: $\mathop{\arg \max}_Y P(X, Y\|\theta)$ 已知模型$\theta$和观测序列$X$, 推出该序列对应的 hidden label Y。这个问题其实就是使用 HMM 模型时的 decode 解码过程，使用了 Viterbi Algorithm，是动态规划算法，注意和 beam search 做区分。因为 HMM 当前状态只依赖于上个状态，所以可以由上个状态得到当前状态的最优解，适合动态规划。forward phase和 Inference 1 相似，只是把 上个时刻所有可能状态之和 替换为 上个状态到当前状态最大概率的值，并且记录下到当前状态所经过的上个状态值。backward phase 是由 forward phase 求出的最后一个时刻的最优状态，根据 forward phase中产生的状态记录，回溯，得到最优状态序列 Y

Learning： $\mathop{\arg \max}_{\theta} P(X\|\theta)$ 模型参数$\theta$未知， 从观测序列 X 学习得到。学习的过程是用了 Baum-Welch algorithm。和 EM 过程一样（迭代 inference 和 re-estimate 过程），先填充未知的参数，做 inference 得到 hidden variable 的值（注意，这边的 inference 不是和前面一样，用的是 Gibbs Sampling 的方法），然后再重新估计参数。重复上述过程直到收敛。

Stochastic Process and Markov property

Markov property 也可以说是 Memoryless property。

给变量增加时间维度$X\rightarrow X^{(t)}$

$$P(X)=\prod_{t=1}^n P(X(t)\|X(1), …, X(t-1))$$

• Markov assumption: $P(X)=\prod_{t=1}^n P(X(t)\|X(t-1))$, 当前时刻只由上个时刻决定

• 分布式稳态的(stationary)，时不变的(time invariant), 同质的(homogeneous)$\forall i, j: P(X(i)\|X(i-1))=P(X(j)\|X(j-1))$

Dynamic Bayesian Networks

Dynamic Bayesian Networks for Time Invariant Process/System

时不变过程/系统的动态贝叶斯网络

通常时不变系统的参数是不会随着时间改变的

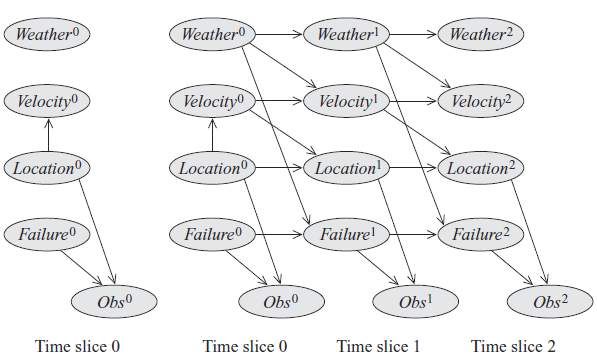
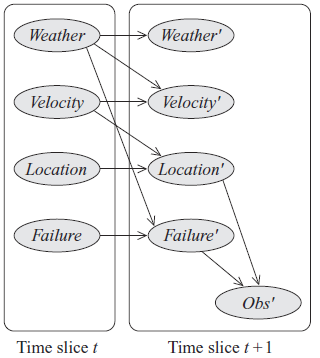
在每个时间片的参数：

• 内部state variables的参数
• state variables 和 observation variables 之间的 emission/observation parameters

transition parameters between two consecutive time slices

Hidden Markov Models(HMMs)

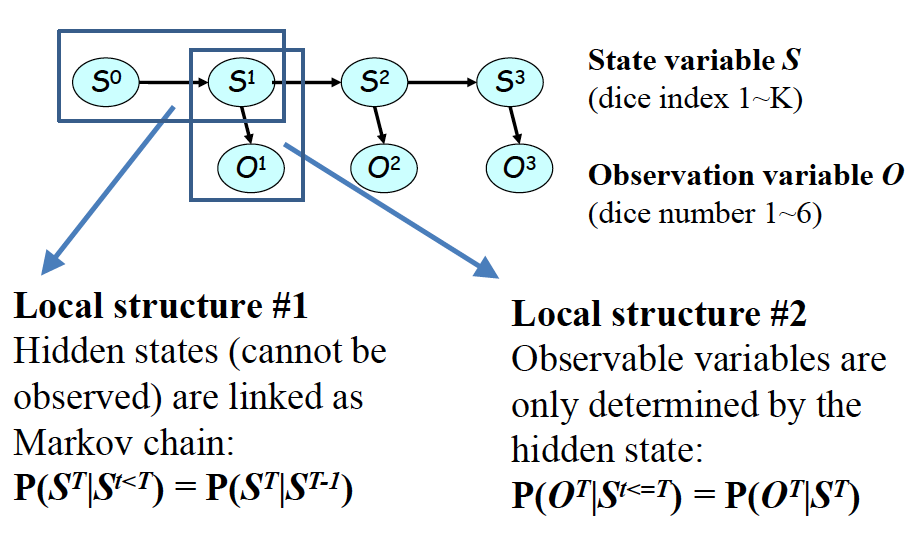
State-Observation Models

如果 hidden variables 可以离散化为若干状态，那么 HMM 可以表示为 State-Observation Models.

• State-State Transmission Matrix T(n, n): $S^t=TS^{t-1}$
• State-Observation Emission Matrix E(m, n): $O^t=ES^t$

A Few Examples of HMM Representations

1. Stock Market Index
2. Chromatin States

Calculations for HMMs

Formal Model Representation

模型参数： $\theta \begin{cases} T=\{t_{i, j}, \quad i, j=1...N\}, Transmission Matrix\\ E=\{e_{i, j}, \quad i=1...N, j=1...K\}, Emission Matrix\\ \pi=\{\pi_i, \quad i=1...N\} Initial State \end{cases}$ 隐状态有 N 个值，观测变量有 K 个取值

观测序列 $X=\{x_t, t=1...T\}$ 基本思想是：$P(X)=\sum_Y P(XY)$

通过分解定律：$P(XY)=P(Y_1)P(X_1\|Y_1)P(Y_2\|Y_1)P(X_2\|Y_2)P(Y_3\|Y_2)...$

所以可以通过不断消掉$Y_i$来解决这个模型

Problem1（Inference）: $P(X|\theta)$ , 已知模型$\theta$和观察序列$X$，推测该模型得到该观测序列的概率

基本思路就是$P(X)=\sum_Y P(XY)$, 从 XY 的联合分布，将 Y 积掉，得到观测序列 X 的概率。而 P(XY)可以根据 HMM 分解：

$$P(XY)=P(Y_1)P(X_1\|Y_1)P(Y_2\|Y_1)P(X_2\|Y_2)...$$

或者$P(XY)=P(X_T\|Y_T)P(Y_{T}\|Y_{T-1})P(X_{T-1}\|Y_{T-1})…$

所以可以从两个方向去吧 $Y_i$消除，一个是从前往后（Forward alogrithm），如上述式子 1，一个是从后往前(Backward algorithm)，如上述式子 2

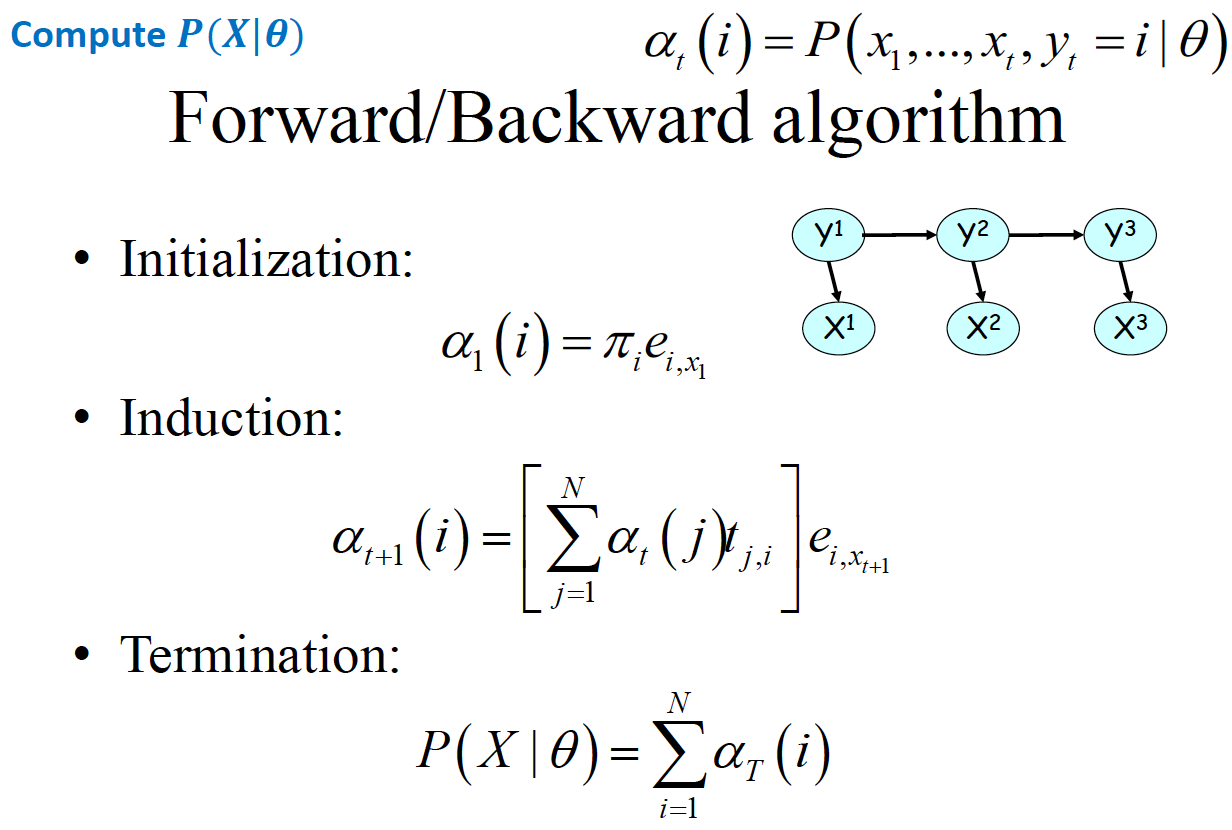
这里的$\pi_i=P(Y_i), e_{i, x_i}=P(X_i\|Y_i), t_{j, i}=P(Y_{i}\|Y_{j})$, 所以$\alpha_{t+1}(i)$不断迭代的过程其实就是在P(XY)的连乘式子上不断添加项，并且做消元，下面另一个方向也是同理。

Problem2（Inference）: $\mathop{\arg \max}_Y P(X, Y|\theta)$ 已知模型$\theta$和观测序列$X$, 推出该序列对应的 hidden label Y

这一步就是求 HMM 中最有可能的状态序列(即概率最大的状态序列 Y)

使用 Viterbi algorithm，这是一个动态规划算法。由于 HMM 的 Markov 性质，当前状态只依赖于上个状态，所以只从上个状态就能推断出当前状态的最优值。

对于$Y_1=i, \delta_{1, i}=\pi_i e_{i, x_1}$ ,$\delta_{t, i}$有点类似于 inference 1 中的$\alpha_t(i)$ ，只不过是$\delta_{t, i}$ 只需要得到最大可能转移值，而不像$\alpha_t(i)$ 将所有转移路径的可能都相加了。非常重要的是，用$\phi_t(i)$记录下了 t 时刻转移到状态 i时是由上个时刻的状态$y_{t-1}$转移过来的。当forward phase 走到最后，可以得到最后时刻的最优状态$y_T^*$ 。进入到 backward phase，可以直接从最后一个状态$y_T^*$和$\phi_T(y_T^*)$得到上个状态$y_{T-1}^*$，依次递推出整个状态序列，结束 backward phase。

Problem3（Learning）: $\mathop{\arg \max}_{\theta} P(X|\theta)$ 模型参数$\theta$未知， 从观测序列 X 学习得到

使用 Baum-Welch algorithm ，也就是 EM。

1. 先初始化参数 $\theta^0=\{T^0, E^0, \pi^0\}$
2. 做 inference（用 Gibbs sampling），推出 hidden values
3. 重新估计新的参数
4. 进行 2 和 3 的迭代，直到收敛

Gibbs sampling is a Markov chain Monte Carlo(MCMC) algorithm for obtaining a sequence of random samples from multivariate probability distribution.

使用 Gibbs sampling 来得到隐变量的概率，其实最后只需要保留和 $y_t$相关的项，即$y_t$的 Markov blanket，然后他们的条件概率相乘就行。然后用采样出来的样本，重新估计新的参数 T 和 E

$$\xi_t(i, j)=P(y_t=i, y_{t+1}=j\|X, \theta)$$

时刻 t 隐状态为 i 的概率：$\gamma_t(i)=\sum_{j=1}^Y \xi_t(i, j)$

状态为 i 的期望：$\sum_{t=0}^{T-1}\gamma_t(i)$

从状态 i 转移到状态 j 的期望：$\sum_{t=0}^{T-1} \xi_t(i, j)$

Generate Simulated Data Using HMMs

MCMC 的一个经典用法是可以近似一个 target distribution。

Extended Models

Factorial HMMs

Hierarchical HMMs

Bayesian HMMs

Max Entropy Markov Models——MEMM

这个模型是结合了 HMM 和 Maximum Entropy。和 HMM 的区别是把从状态到观测值的方向掉了个头，是从观测值来推出隐状态。所以是一个 discriminative model。