Chap2 Bayesian Networks: Representation

Conditional independence

变量 X 和 Y 是独立的：

$P(X=x\|Y=y)=P(X=x)$ 即Y的取值不会改变X的预测概率

$$P(X, Y) = P(X\|Y)P(Y) = P(X) P(Y)$$ $$P(X_1, …, X_n)=P(X_1)…P(X_n)$$

变量 X 和 变量 Y 在给定 Z的条件下是条件独立(conditionally independent)的

P(X=x|Y=y, Z=z) = P(X=x|Z=z) for all values x, y, z

可以写作：$Ind(X;Y\|Z) or (X\bot Y\|Z)$

Conditional Parameterization

这一节是说如何计算条件概率的参数量

比如P(D, I, G)=P(D)P(I)P(G|D, I) 其中D和I是二值变量，G是三值变量，所以P(D)和P(I)都是1个独立参数，而P(G|D, I)有4*(3-1)=8个独立参数，4是D和I有4种组合，G是三值，所以知道两个概率就可以求出剩下一个的概率，所以是2个参数

Naive Bayes model

$$P(C, X_1, …, X_n)=P(C)\prod_{i=1}^n P(X_i\|C)$$

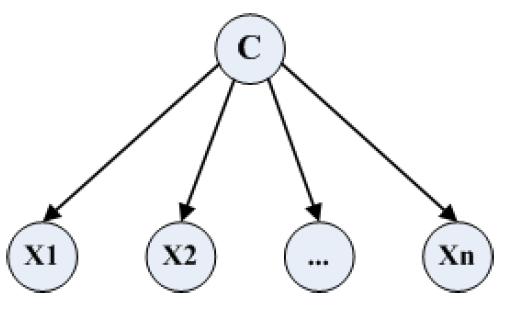
Baysian networks

BNs and local independences

有向无环图 DAG G 编码了 local independence assumptions:

$$(X_i \bot NonDesc(X_i) \| Pa(X_i))$$

给定父亲节点，$X_i$ 独立于它的非后继节点(即独立于它的 Markov Blanket)

I-map and factorization

I-Maps: Independency Mappings

P 是 X 的分布

I(P)是 P 上的 independencies(不知道怎么用中文表示。。。)

A Bayesian network G is an I-map of P if I(G) $\subseteq$ I(P) $\leftrightarrow P(X_1, …, X_n)=\prod_{i=1}^n P(X_i\|Pa(X_i))$

所以上面这句话就是说如果符合G 的 independence 是符合 P 的 inpendencies 的子集，那么 G 就是 P 的 I-Map。

G 是 P 的 I-Map，P 可以根据 G 做分解

P可以根据 G 做分解，那说明 G 是 P 的 I-Map

Bayesian Network其实是由(G，P)共同定义的，P 在 G 上做分解（BN Factorization），P 定义为关于 G 上节点的conditional probability dependences（CPDs）的集合

一个很简单的计算题：符合P(X, Y, C) = P(C)P(X|C)P(Y|C) 的G

计算 P(X=x|Y=y), 要讲 C 加入到这个计算式子中，如何加呢？

$$P(x\|y)=\sum_c P(x, C\|y)$$

给定 y分解x 和 C

$$P(x\|y)=\sum_c P(x, c\|y)=\sum_c P(x\|y, c)P(c\|y)$$

因为$(X\bot Y\|C)$ P(x|y, c)=P(x|c)

$$P(x\|y)=\sum_c P(x, c\|y)=\sum_c P(x\|y, c)P(c\|y)=\sum_c P(x\|c) P(c\|y)$$

P(c|y)使用贝叶斯公式

$$P(x\|y)=\sum_c P(x, c\|y)=\sum_c P(x\|y, c)P(c\|y)=\sum_c P(x\|c) P(c\|y)=\sum_c P(x\|c) \frac{P(y\|c)P(c)}{\sum_c P(y\|c)P(c)}$$

上述整个过程其实就是努力把公式的所有项都转化为”local probability”的形式 P(child|Parents)

d-separation in BNs

其实就是设计一个过程能找到 G 中的所有 independencies

直接相连的 X 和 Y 是 not separated

active：X 和Y 之间的路是通的，是相互依赖的，非独立的

blocked：X 和 Y 之间的路被堵住了，是相互独立的

令$X_1\leftrightarrow … \leftrightarrow X_n$是 G 的一条 trail 路径，E是 G 的观测节点(evidence nodes)子集

The trail $X_1\leftrightarrow … \leftrightarrow X_n$ is active given evidence E if:

• For every V-structure $X_{i-1} \rightarrow X_i \leftarrow X_{i+1}$ , $X_i$ or one of its descendants is observed

• No other nodes along the trail are in E

给定 Z, 如果没有 active trail 在X 和 Y 之间，X 和 Y 是 d-separeted in G ，记作$d-sep_G (X;Y\|Z)$

从d-separation 可以得到所有的 independencies

backward process：给出结果，推断原因(learning的过程)，更难

forward process：从原因到结果(inference 的过程)

为什么 backward 更难呢，在 v-structure, 因为子节点观测到的话，会 activate the trails(probability dependences) between their parents，而且这种依赖还会继续往上传递。但是树状结构不就是没有 v-structure 吗

有个 d-separation 的算法来找到给定观测变量 Z，找到X所有 reachable 的 nodes

有了更多的独立关系，可以减少参数量，而且对于 inference，只需要考虑子图上的 loca dependent

Two graph G1 and G2 are I-equivalent, if I(G1)=I(G2)

这两个图encode 的独立关系相同

From distribution to BNs

即从分布 P，构造出图 G，能够合理替代分布 P 中的独立性

Minimal I-Maps

A graph G is a minimal I-map for a set of independences I if it is an I-map for I, and if the removal of even a single edge from G renders it not an I-map.

移除一条边意味着增加独立条件。

主要思想是，对于第 i 个变量$X_i$, 从前面 i-1个变量中找到$X_i$父亲节点的最小集合。

对于变量不同的初始排列顺序会生成不同的网络 G

Perfect Maps

A graph G is a perfect map (P-map) for a set of independences I if I(G)=I or I(G)=I(P). P is a distribution

枚举G和 P所有的独立条件，看是否 G 是 P 的 perfect map