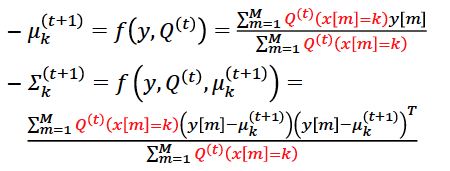概率图学习——Learning with incomplete data 从部分观测数据学习

Variables are Not Detectable

为什么变量是不能观测到的呢？因为变量可能是 hidden variables，不能被观测，只是一个概念，非真实存在。

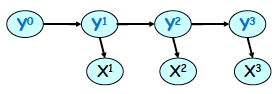
在这里插入图片描述

状态变量 y 不能被观测

在这里插入图片描述

缺失值和异常点，系统可能会没有检测到一些观测点。还有一些异常点。

对一个MLE 框架下，已知数据 D={y[1],…,y[M]}

目标函数：$\underset{\theta}{\operatorname{arg max}} p(D|\theta)$

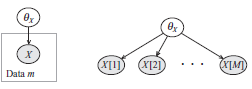
在这里插入图片描述

对于完整数据，MLE 学习是简单的，已知完整数据 Dc={(x[i], y[i])}~i=1…M~

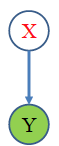
在这里插入图片描述

E-step:

x的先验分布π~k~ = p(X=k): $\pi_k^*=\frac{M[x=k]}{M}$

M-step:

$\mu_k^*=\frac{1}{M[x=k]}\sum_m y[m] |_{x[m]=k}$

$\Sigma_k^=\frac{1}{M[x=k]}\sum_m (y[m]-\mu_k^)(y[m]-\mu_k^*)^T |_{x[m]=k}$

但是实际上X 是不知道的，只有 Y 被观测到。

如果我们知道参数θ，可以求得 X 的后验分布（这是 inference 过程）

$Q(x=k)=P(x=k\|y, \theta)=\frac{p(y\|x=k, \theta)p(x=k\|\theta)}{\sum_{k=1}^{K} p(y\|x=k, \theta)p(x=k\|\theta)}$

将 x 的先验分布P(X)=π和 Y 的 likelihood P(Y|X=k)=N~k~^(t)^(Y)代入上式, 得到：

$Q(x[m]=k)=\frac{\pi_k^{(t)}N_k^{(t)}(y[m])}{\sum_{k=1}{K}\pi_k^{(t)}N_k^{(t)}(y[m])}$

其中$N_k^{(y)}=\frac{1}{\sqrt{|2\pi \Sigma|}}exp{-\frac{1}{2}(y-\mu_k)^T\Sigma^{-1}(y-\mu_k)}$

新一轮的 E 步迭代，使用 MLE 更新

计算$Q^{(t)}(x[m]=k)$, 代入下面式子

$\pi_k^{t+1}=\frac{1}{M}\sum_{m=1}^M Q^{(t)}(x[m]=k)$

新一轮的 M 步迭代：

在这里插入图片描述