L1, L2 正则化

正则化是防止过拟合的一个手段，降低模型复杂度，让解更简单——Occam’s Razor。

以 LR 为例，LR 的原目标函数：$\min \frac{1}{N} \sum_{i=1}^N (y_i - w^Tx_i)^2$

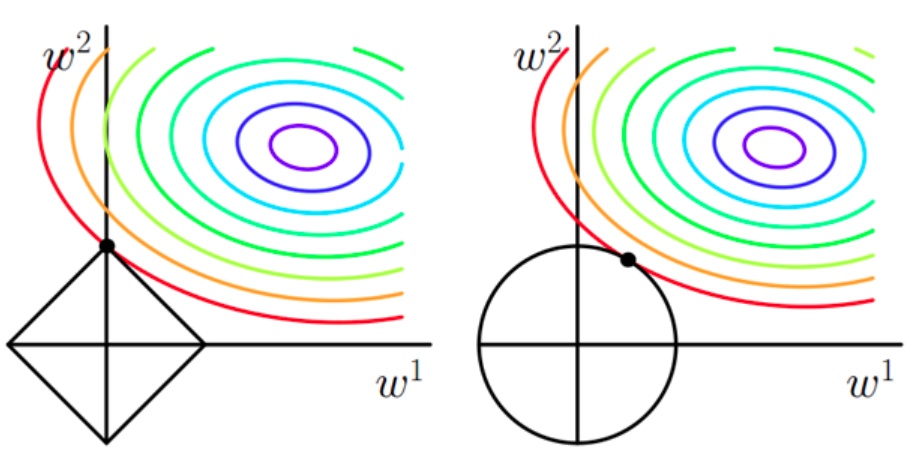
彩色的等高线是 LR 原目标函数的等高线，越往紫色的值越小

L1 正则项

在 LR 中加了 L1 正则项的叫 Lasso 回归：$\min \frac{1}{N} \sum_{i=1}^N (y_i - w^Tx_i)^2 + C\|w\|_1$

如果以bayesian prior probability 的角度，参数 w~laplace 分布

原曲线的值要小，即接近中心的点

菱形越小越好，$w_1+w_2=K$ 越小越好

由于很多原函数登高曲线和菱形相交容易在坐标轴上，所以解的某些维度容易是 0，例如 w=(0, w2)或者(w1, 0)，0 解多，从而 L1 更容易得到稀疏解。

L2 正则项

在 LR 中加了 L2 正则项的叫 Ridge 回归：$\min \frac{1}{N} \sum_{i=1}^N (y_i - w^Tx_i)^2 + C\|w\|_2$

如果以bayesian prior probability 的角度，参数 w~正态分布

原曲线的值要小，即接近中心的点

菱形越小越好，$w_1^2+w_2^2=K$ 越小越好

相交点会比较靠近坐标轴。L2 能让解比较小（靠近 0），比较平滑（≠0）