统计机器学习 chap1

KNN k 近邻 无参方法

KNN (k-Nearest Neighbor) k 近邻算法。

方法思路：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。

KNN算法中，所选择的邻居都是已经正确分类的对象（已知的训练数据）。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 KNN方法虽然从原理上也依赖于极限定理，但在类别决策时，只与极少量的相邻样本有关。由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。

KNN算法不仅可以用于分类，还可以用于回归。通过找出一个样本的k个最近邻居，将这些邻居的属性的平均值赋给该样本，就可以得到该样本的属性。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值(weight)，如权值与距离成反比。

$$\hat{y}=\sum_{i\in \mathcal{N_K}} \frac{1}{dist(x, x_i)} y_i$$

如果拥有无穷的数据，KNN 的错误率最多是最小错误率(Bayes 错误率)的两倍 (注：Bayes 错误率是给定分布的数据能达到的最小错误率)

KNN的问题：

1. 对于训练集大的问题，计算量太大，因为每分类一个测试样本都要遍历一次训练集，但是用好的近邻搜索策略会减少计算量。
2. K 的选择
3. 距离测量标准很重要

SVM 支持向量机 有参方法

二元分类可以看做是在特征空间中将不同类别分割开来。

$$f(x) = sign(w^Tx+b)$$

线性分割

如何分割才是最优的呢？

从样本 $x_i$到分割面的距离是$r = \frac{\|w^Tx_i+b\|}{\|w\|}$

最靠近超平面(hyperplane)的样本就是支持向量(support vectors)

分割面的间隔(margin $\rho$)就是支持向量超平面之间的距离

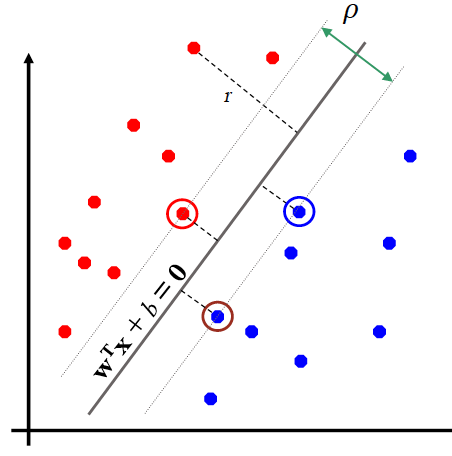
所以分类的 $confidence=y_i(w^Tx_i+b)$

尽量使得 margin 更大，而之前定义是 margin 是支持向量超平面之前的距离，所以只涉及支持向量，其他训练数据是无关的

线性 SVM

设训练集被间隔为$\rho$ 的超平面分割

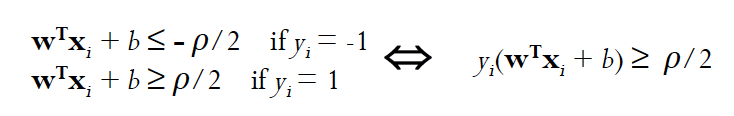
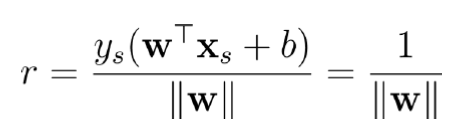
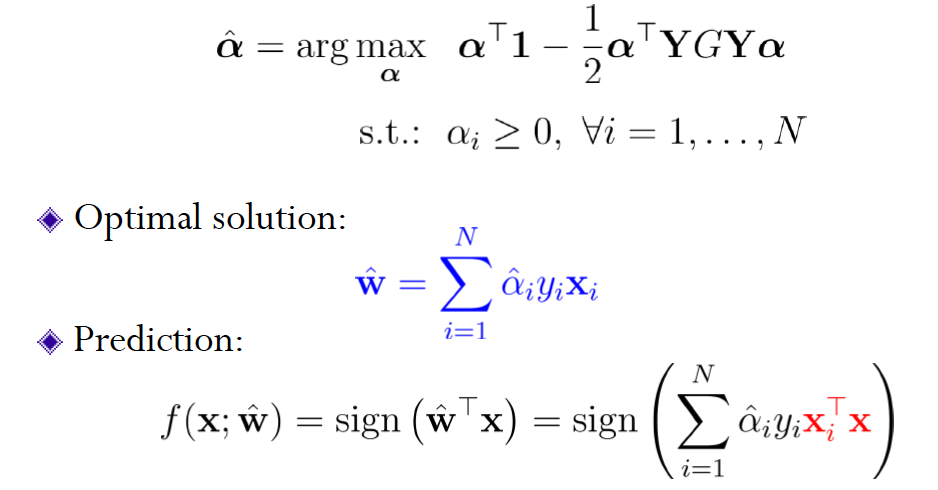
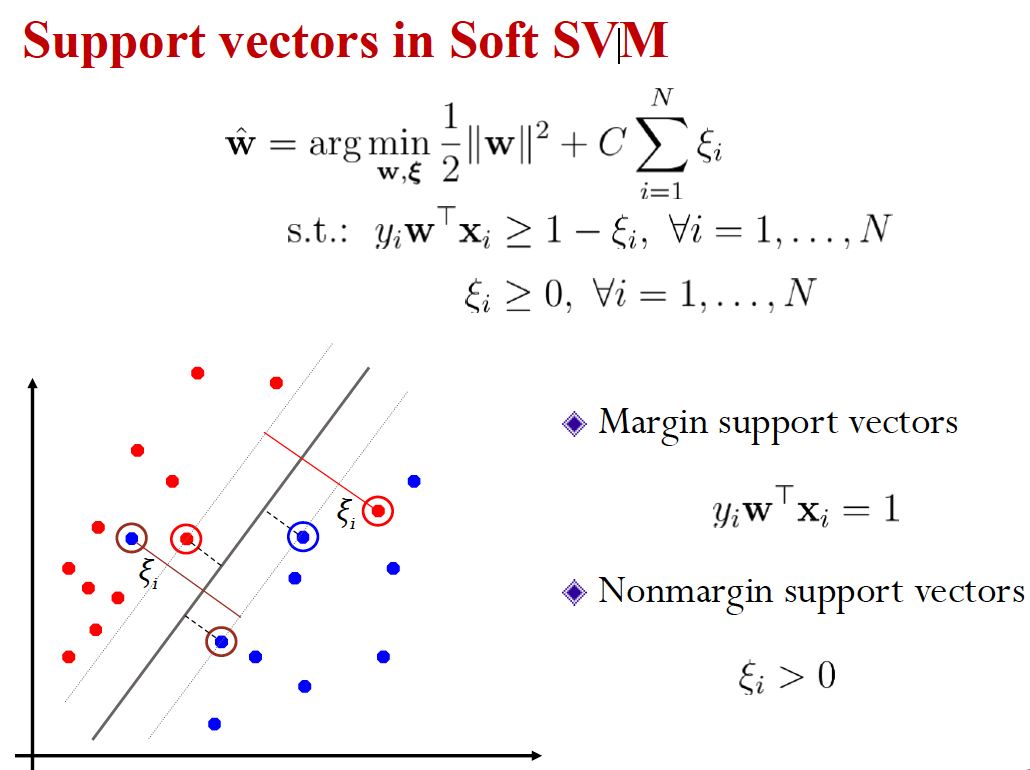
对支持向量$x_s$来说，上式不等式是一个等式，在用$\rho$/2放缩 w 和 b后，$y_i(w^Tx_i+b) \geq 1, \forall i=1, …, N$

上面是 hard SVM(使用 hard 约束条件，必须线性可分) ，但是有些无法线性分割，一个方法是增加新的特征，使之在高维空间是线性可分的

另一个是使用 soft margin SVM 而不是 hard SVM

但是因为阶跃函数非凸，所以想用其他函数替代，比如

$\ell_{lin}(yf(x))=max(0, 1-yf(x))$ Hinge loss, convex, non-smooth

$\ell_{quad}(yf(x))=max(0, 1-yf(x))^2$ Square-loss, convex, smooth

$\ell_{Huber}(yf(x))=\begin{cases}1-yf(x) \quad if \quad yf(x) < 0 \\ max(0, 1-yf(x))^2,\quad if \quad yf(x) \geq 0\end{cases}$ 结合了上面两种方法，convex, smooth

如果用 hinge loss 来代替 0-1 loss，可以求得 0-1loss 的 upper bound

为什么 Support Vector Machine 叫这个名字？

是因为在 Hard-SVM 中，KKT 条件中的一条就是所有 support vectors $x_i$ ,满足$y_i \hat{w} x_i =1$

NonLinear SVM

把数据映射到高维空间中，使得在高维空间中训练数据是可分割的。

Kernel Trick: 映射函数，找另一种表示，在 SVM 和无监督学习中都有同样的思想

$$\Phi(x)^T \Phi(z) = (x^Tz)^d=K(x,z)$$

核函数，相当于是等于在特定特征空间的内积。而且不需要映射到高维空间后再做点积，直接用 K 计算点积

Mercer’s theorem:

任意半正定对称函数都是核函数

常用核函数：

1. 线性：$K(x_i, x_j)=x_i^Tx_j$ $\Phi: x \rightarrow \Phi(x)$ where $\Phi(x)=x$
2. p 次多项式：$K(x_i, x_j)=(1+x_i^Tx_j)^p$
3. 高斯：$K(x_i, x_j)=exp(-\frac{\|x_i-x_j\|^2}{2\sigma})$

Holdout Method

用 Resampling 来解决数据太少，测试集很宝贵的情况

1. Cross-validation
   1. Random subsampling
   2. K-fold cross-validation
   3. Leave-one-out cross-validation
2. Boostrap

选取 fold 的数量是有讲究的，在实际应用中，大数据集用小的 K，而稀疏数据集需要更大的 K

一般 K-fold CV 用 K=10 比较多