梯度消失、爆炸

梯度消失与梯度爆炸其实是一种情况。

梯度消失在两种情况下经常出现:

一是在深层网络中
二是采用了不合适的损失函数，比如sigmoid。

梯度爆炸一般出现在深层网络和权值初始化值太大的情况下。

根本的问题其实并非是梯度消失问题或者梯度激增问题，而是在前面的层上的梯度是来自后面的层上项的乘积。当存在过多的层次时，就出现了内在本质上的不稳定场景。

深度网络角度

根据链式求导法则，更新梯度信息。其中一项是对激活函数进行求导，如果此部分大于1，那么层数增多的时候，最终的求出的梯度更新将以指数形式增加，即发生梯度爆炸，如果此部分小于1，那么随着层数增多，求出的梯度更新信息将会以指数形式衰减，即发生了梯度消失。

总结：从深层网络角度来讲，不同的层学习的速度差异很大，表现为网络中靠近输出的层学习的情况很好，靠近输入的层学习的很慢，有时甚至训练了很久，前几层的权值和刚开始随机初始化的值差不多。因此，梯度消失、爆炸，其根本原因在于反向传播训练法则，属于先天不足

RNN 网络

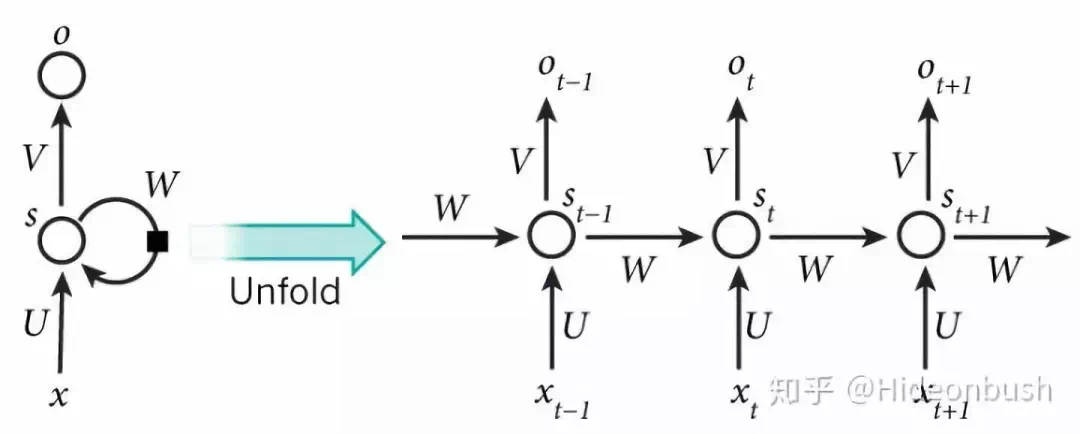
对于RNN的梯度下降方法，是一种基于时间的反向求导算法（BPTT），RNN的表达式： $\begin{array} {c}{s_{t}=\tanh \left(U x_{t}+W s_{t-1}\right)} \\ o_t=\operatorname{softmax}\left(\mathrm{Vs}_{\mathrm{t}}\right)\\ L=\sum_{i=1}^{T}-\overline{o_{t}} \log o_{t}，T 是序列长度 \end{array}$ 有三个参数 U、W、V，对 t=3时刻的 U、W、V 求偏导，由链式法则得到： $\frac{\partial L_{3}}{\partial U}=\sum_{k=0}^{3} \frac{\partial L_{3}}{\partial o_{3}} \frac{\partial o_{3}}{\partial s_{3}} \frac{\partial s_{3}}{\partial s_{k}} \frac{\partial s_{k}}{\partial U}=\sum_{k=0}^{3} \frac{\partial L_{3}}{\partial o_{3}} \frac{\partial o_{3}}{\partial s_{3}}\left(\prod_{j-k-1}^{3} \frac{\partial s_{j}}{\partial s_{j-1}}\right) \frac{\partial s_{k}}{\partial U}$

$\frac{\partial L_{3}}{\partial W}=\sum_{k=0}^{t} \frac{\partial L_{3}}{\partial o_{3}} \frac{\partial o_{3}}{\partial s_{3}}\left(\prod_{j=k-1}^{t} \frac{\partial s_{j}}{\partial s_{j-1}}\right) \frac{\partial s_{k}}{\partial W}$ $\frac{\partial L_{3}}{\partial V}=\frac{\partial L_{3}}{\partial o_{3}} \frac{\partial o_{3}}{\partial V}$

对 V 求偏导不存在依赖问题。但是对于 W、U 求偏导时，存在长期依赖。

激活函数

激活函数 $\phi$ 通常是 tanh: $\prod_{j=k-1}^{3} \frac{\partial s_{j}}{\partial s_{j-1}}=\prod_{j=k-1}^{3} \tanh ^{\prime} W$

激活函数是 tanh 函数时，tanh 函数的导数最大值为 1，大部分都是小于 1 的数在做累乘，若当 t 很大时， $\prod_{j=k-1}^{3} \tanh ^{\prime} W$ 中 $\prod_{j=k-1}^{3} \tanh ^{\prime}$ 趋于 0

权值共享

而RNN还存在一个权值共享的问题，即这几个 W 都是一个，假设，存在一个反复与 W 相乘的路径，t步后，得到向量：

$\prod_{j=k-1}^{3} \frac{\partial s_{j}}{\partial s_{j-1}}=\prod_{j=k-1}^{3} \tanh ^{\prime} W$

若特征值大于1，则会出现梯度爆炸。

若特征值小于1，则会出现梯度消失。

因此在一定程度上，RNN 对比 BP 更容易出现梯度问题。主要是因为 RNN 处理时间步长一旦长了，W 求导的路径也变的很长，即使 RNN 深度不大，也会比较深的 BP 神经网络的链式求导的过程长很大。

另外，对于共享权值 W，不同的 Wi 相乘也在一定程度上可以避免梯度问题。

悬崖和梯度爆炸

对于目标函数，通常存在梯度变化很大的一个“悬崖”，在此处求梯度，很容易导致求解不稳定的梯度爆炸现象。

激活函数角度

计算权值更新信息的时候需要计算前层偏导信息，因此如果激活函数选择不合适，比如使用sigmoid，梯度消失就会很明显了。

如果使用 sigmoid 作为损失函数，其梯度是不可能超过0.25的，这样经过链式求导之后，很容易发生梯度消失。

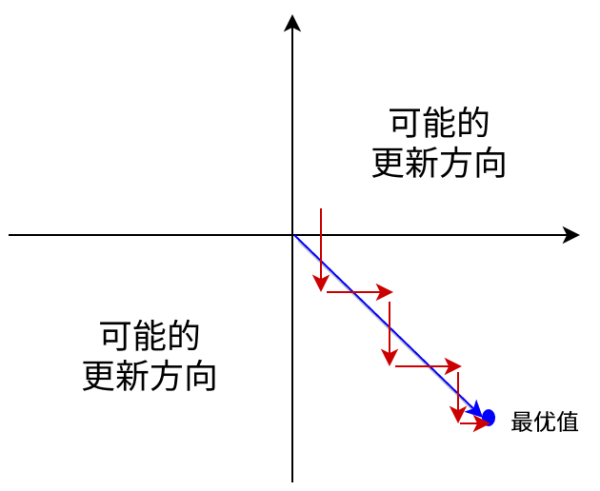
而且 sigmoid 的输出值恒大于 0，会导致模型训练的收敛速度变慢。因为梯度更新会出现 zigzag 现象。对 $\sigma(\sum w_i x_i + b)$ 来说，如果 $x_i$ 均为正数或负数，那么对 $w_i$ 的导数总是正数或负数，这回导致如下图红色箭头所示的阶梯式更新，这显然并非一个好的优化路径。深度学习往往需要大量时间来处理大量数据，模型的收敛速度是尤为重要的。所以，总体上来讲，训练深度学习网络尽量使用zero-centered数据 (可以经过数据预处理实现) 和zero-centered输出。

同理，**tanh **作为激活函数，它的导数图如下，可以看出，tanh 比 sigmoid 要好一些，但是它的导数仍然是小于1的。tanh 数学表达为： $\tanh (x)=\frac{e^{x}-e^{-x}}{e^{z}+e^{-x}}$

优点解决了zero-centered的输出问题。
缺点梯度消失的问题和幂运算的问题仍然存在。

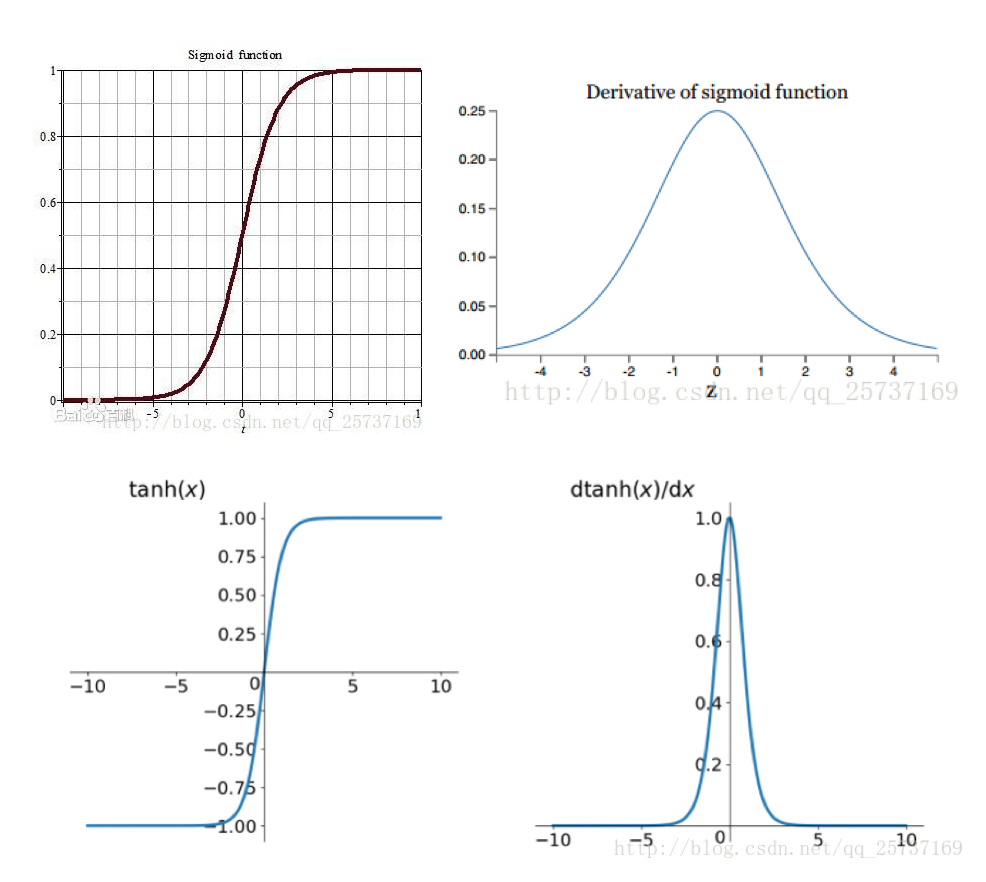
事实上，梯度消失更容易出现，因为对于激活函数的求导：

$\sigma^{\prime}(w x+b)$

当w越大，其wx+b很可能变的很大，而根据上面sigmoid函数导数的图像可以看到，wx+b越大，导数的值也会变的很小。因此，若要出现梯度爆炸，其w既要大还要保证激活函数的导数不要太小。

解决方案

pre-train+finetune

此方法来自Hinton在2006年发表的一篇论文，Hinton为了解决梯度的问题，提出采取无监督逐层训练方法，其基本思想是每次训练一层隐节点，训练时将上一层隐节点的输出作为输入，而本层隐节点的输出作为下一层隐节点的输入，此过程就是逐层“预训练”（pre-training）；在预训练完成后，再对整个网络进行“微调”（fine-tunning）。Hinton在训练深度信念网络（Deep Belief Networks中，使用了这个方法，在各层预训练完成后，再利用BP算法对整个网络进行训练。此思想相当于是先寻找局部最优，然后整合起来寻找全局最优，此方法有一定的好处，但是目前应用的不是很多了

梯度clipping

梯度剪切这个方案主要是针对梯度爆炸提出的，其思想是设置一个梯度剪切阈值，然后更新梯度的时候，如果梯度超过这个阈值，那么就将其强制限制在这个范围之内。这可以防止梯度爆炸。

正则

权重正则化（weithts regularization）比较常见的是 l1 正则，和 l2 正则

正则化是通过对网络权重做正则限制过拟合，仔细看正则项在损失函数的形式： $\text {Loss}=\left(y-W^{T} x\right)^{2}+\alpha\|W\|^{2}$ 其中，α 是指正则项系数，因此，如果发生梯度爆炸，权值的范数就会变的非常大，通过正则化项，可以部分限制梯度爆炸的发生。

注：事实上，在深度神经网络中，往往是梯度消失出现的更多一些。

Relu 等激活函数

Relu

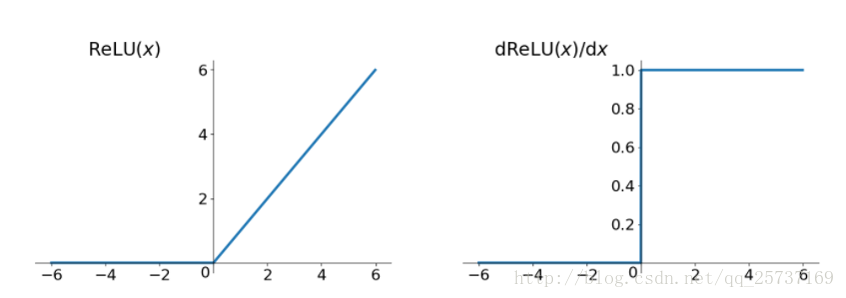
Relu 思想也很简单，如果激活函数的导数为 1，那么就不存在梯度消失爆炸的问题了，每层的网络都可以得到相同的更新速度，relu 就这样应运而生。先看一下 relu 的数学表达式： $\operatorname{Relu}(\mathrm{x})=\max (\mathrm{x}, 0)=\left\{\begin{array}{l}{0, x<0} \\ {x, x>0}\end{array}\right\}$

relu函数的导数在正数部分是恒等于1的，因此在深层网络中使用relu激活函数就不会导致梯度消失和爆炸的问题。

relu的主要贡献在于：

解决了梯度消失、爆炸的问题（在正区间）
计算方便，计算速度快（只需要判断输入是否大于 0）
加速了网络的训练（收敛速度远快于 sigmoid 和 tanh）

同时也存在一些缺点：

Dead ReLU problem: 由于负数部分恒为0，会导致一些神经元无法激活，导致相应的参数永远不能被更新（可通过设置小学习率部分解决）有两个主要原因可能导致这种情况产生:
- 非常不幸的参数初始化，这种情况比较少见
- 学习速率太高导致在训练过程中参数更新太大，不幸使网络进入这种状态
- 解决方法：
  - 采用Xavier初始化方法
  - 避免将学习速率设置太大
  - 使用adagrad等自动调节学习速率的算法。
输出不是以0为中心的（zero-centered）

Leak Relu

leak relu就是为了解决ReLU的0区间带来的影响，其数学表达为: $\text {leak relu}=\max (k * x, x)$ 其中k是leak系数，一般选择0.01或者0.02，或者通过学习而来。

leak relu解决了0区间带来的影响，而且包含了relu的所有优点

elu

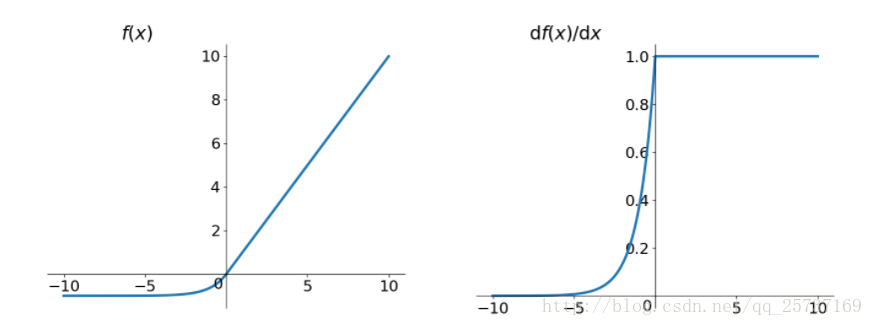
elu(Exponential Linear Units)激活函数也是为了解决relu的0区间带来的影响，其数学表达为: $\left\{\begin{array}{cc}{x,} & {\text { if } x>0} \\ {\alpha\left(e^{x}-1\right),} & {\text { otherwise }}\end{array}\right.$

但是elu相对于leakrelu来说，计算要更耗时间一些

ELU也是为解决ReLU存在的问题而提出，显然，ELU有ReLU的基本所有优点，以及：

不会有Dead ReLU问题
输出的均值接近0，zero-centered

BatchNormalization

Batchnorm 具有加速网络收敛速度，提升训练稳定性的效果。

Batchnorm 本质上是解决反向传播过程中的梯度问题，通过规范化操作将输出信号 x 规范化保证网络的稳定性。

反向传播中，经过每一层的梯度会乘以该层的权重w，举个简单例子：正向传播中 $f2=f1(w^Tx+b)$ , 那么反向传播中， $\frac{\partial f_{2}}{\partial x}=\frac{\partial f_{2}}{\partial f_{1}} w$ ，反向传播式子中有w的存在，所以w的大小影响了梯度的消失和爆炸。

batchnorm就是通过对每一层的输出规范为均值和方差一致的方法，消除了w带来的放大缩小的影响，进而解决梯度消失和爆炸的问题，或者可以理解为BN将输出从饱和区拉倒了非饱和区。

残差结构

事实上，就是残差网络的出现导致了image net比赛的终结，自从残差提出后，几乎所有的深度网络都离不开残差的身影，相比较之前的几层，几十层的深度网络，在残差网络面前都不值一提，残差可以很轻松的构建几百层，一千多层的网络而不用担心梯度消失过快的问题，原因就在于残差的捷径（shortcut）部分，其中残差单元如下图所示：

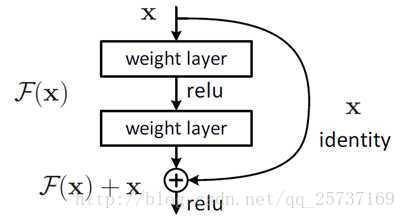
相比较于以前网络的直来直去结构，残差中有很多这样的跨层连接结构，这样的结构在反向传播中具有很大的好处，见下式： $\frac{\partial l o s s}{\partial x_{l}}=\frac{\partial \operatorname{loss}}{\partial x_{L}} \cdot \frac{\partial x_{L}}{\partial x_{l}}=\frac{\partial \operatorname{loss}}{\partial x_{L}} \cdot\left(1+\frac{\partial}{\partial x_{L}} \sum_{i=l}^{L-1} F\left(x_{i}, W_{i}\right)\right)$ 式子的第一个因子 $\frac{\partial \operatorname{loss}}{\partial x_{L}}$ 表示的损失函数到达 L 的梯度，小括号中的1表明短路机制可以无损地传播梯度，而另外一项残差梯度则需要经过带有weights的层，梯度不是直接传递过来的。残差梯度不会那么巧全为-1，而且就算其比较小，有1的存在也不会导致梯度消失。所以残差学习会更容易。

LSTM

LSTM全称是长短期记忆网络（long-short term memory networks），是不那么容易发生梯度消失的，主要原因在于LSTM内部复杂的“门”(gates)，如下图，LSTM通过它内部的“门”可以接下来更新的时候“记住”前几次训练的”残留记忆“，因此，经常用于生成文本中。

LSTM 公式： $\begin{aligned} f_{t} &=\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right) \\ i_{t} &=\sigma\left(W_{i} \cdot\left[h_{t-1}, x_{t}\right]+b_{i}\right) \\ {C}'_{t} &=\tanh \left(W_{C} \cdot\left[h_{t-1}, x_{t}\right]+b_{C}\right) \\ C_{t} &=f_{t} * C_{t-1}+i_{t} * {C}'_{t} \\ o_{t} &=\sigma\left(W_{o}\left[h_{t-1}, x_{t}\right]+b_{o}\right) \\ h_{t} &=o_{t} * \tanh \left(C_{t}\right) \end{a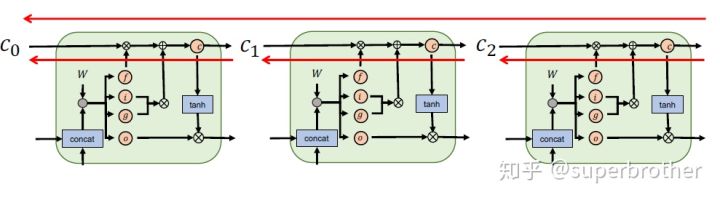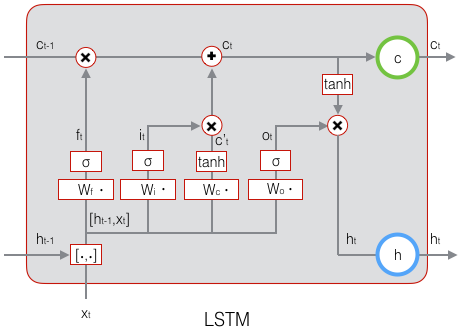ligned}$ 由于 sigmoid 的输出 f(t) 在[0,1]之间，因此这里的输出 $f_t$ 代表了遗忘上一层隐藏细胞状态的概率

这样，我们就把LSTM关于当前的记忆（ $i_{t} * {C}'_{t}$ ）和长期的记忆( $f_{t} * C_{t-1}$ )组合在一起，形成了新的单元状态( $C_t$ )。

由于遗忘门的控制，它可以保存很久很久之前的信息。

由于输入门的控制，它又可以避免当前无关紧要的内容进入记忆。

输出门控制了长期记忆对当前输出的影响。LSTM最终的输出，是由输出门和单元状态共同确定的。

下文引用自4

但是“LSTM 能解决梯度消失/梯度爆炸”是对 LSTM 的经典误解。

首先需要明确的是，RNN 中的梯度消失/梯度爆炸和普通的 MLP 或者深层 CNN 中梯度消失/梯度爆炸的含义不一样。
1. MLP/CNN 中不同的层有不同的参数，各是各的梯度；
2. 而 RNN 中同样的权重在各个时间步共享，最终的梯度 g = 各个时间步的梯度 g_t 的和。
由 1 中所述的原因，RNN 中总的梯度是不会消失的。即便梯度越传越弱，那也只是远距离的梯度消失，由于近距离的梯度不会消失，所有梯度之和便不会消失。RNN 所谓梯度消失的真正含义是，梯度被近距离梯度主导，导致模型难以学到远距离的依赖关系。
LSTM 中梯度的传播有很多条路径， $c_{t-1} \rightarrow c_{t}=f_{t} \odot c_{t-1}+i_{t} \odot \hat{c}_{t}$ 这条路径上只有逐元素相乘和相加的操作，梯度流最稳定；但是其他路径（例如 $c_{t-1} \rightarrow h_{t-1} \rightarrow i_{t} \rightarrow c_{t}$ 上梯度流与普通 RNN 类似，照样会发生相同的权重矩阵反复连乘。
LSTM 刚提出时没有遗忘门，或者说相当于 $f_{t}=1$ ，这时候在 $c_{t-1} \rightarrow c_{t}$ 直接相连的短路路径上，可以无损地传递给 $d l / d c_{t-1}$ ，从而这条路径上的梯度畅通无阻，不会消失。类似于 ResNet 中的残差连接。
但是在其他路径上，LSTM 的梯度流和普通 RNN 没有太大区别，依然会爆炸或者消失。
1. 由于总的远距离梯度 = 各条路径的远距离梯度之和，即便其他远距离路径梯度消失了，只要保证有一条远距离路径（就是上面说的那条高速公路）梯度不消失，总的远距离梯度就不会消失（正常梯度 + 消失梯度 = 正常梯度）。因此 LSTM 通过改善一条路径上的梯度问题拯救了总体的远距离梯度。
2. 同样，由于总的远距离梯度 = 各条路径的远距离梯度之和，高速公路上梯度流比较稳定，但其他路径上梯度有可能爆炸，此时总的远距离梯度 = 正常梯度 + 爆炸梯度 = 爆炸梯度，因此 LSTM 仍然有可能发生梯度爆炸。不过，由于 LSTM 的其他路径非常崎岖，和普通 RNN 相比多经过了很多次激活函数（导数都小于 1），因此 LSTM 发生梯度爆炸的频率要低得多。实践中梯度爆炸一般通过梯度裁剪来解决。
对于现在常用的带遗忘门的 LSTM 来说，5.2 中的分析依然成立，而 5.1 分为两种情况：
1. 其一是遗忘门接近 1（例如模型初始化时会把 forget bias 设置成较大的正数，让遗忘门饱和），这时候远距离梯度不消失；
2. 其二是遗忘门接近 0，但这时模型是故意阻断梯度流的，这不是 bug 而是 feature（例如情感分析任务中有一条样本 “A，但是 B”，模型读到“但是”后选择把遗忘门设置成 0，遗忘掉内容 A，这是合理的）。
3. 当然，常常也存在 f 介于 [0, 1] 之间的情况，在这种情况下只能说 LSTM 改善（而非解决）了梯度消失的状况。

梯度消失和梯度爆炸