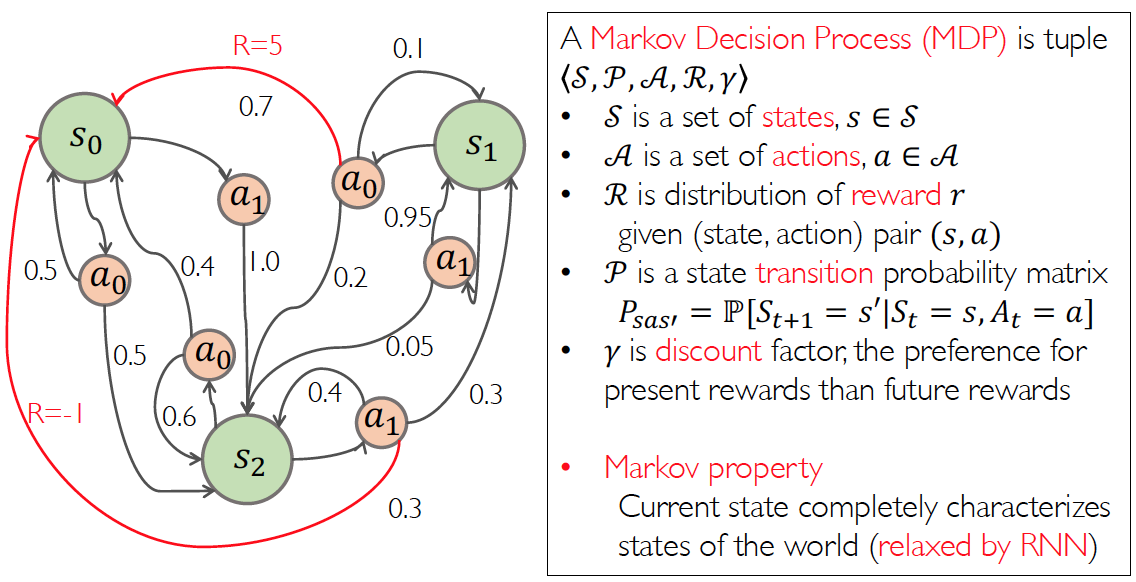
Markov Decision Process(MDP)

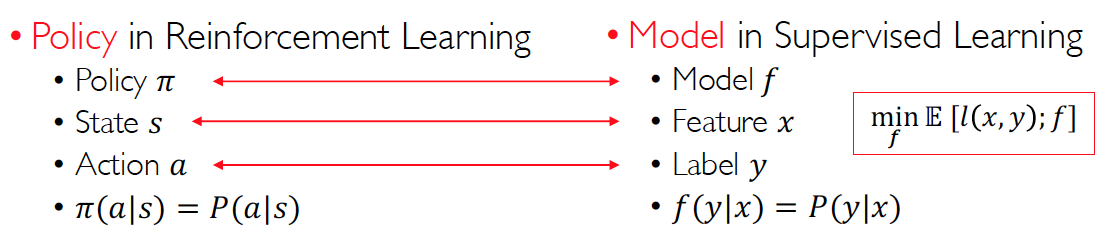
Policy

A policy $\boldsymbol{\pi} : \mathcal{S} \rightarrow \mathcal{A}$ specifies what action to take in each state

• Deterministic policy: $a=\pi(s)$ (for a state, only one action is taken)
• Stochastic policy: $\pi(a \| s)=P(a \| s)$ (requires sampling to take action)

Objective: find optimal $\boldsymbol{\pi}^{*}$ to maximize the expected sum of rewards $\pi^{*}=\operatorname{argmax} \mathbb{E}\left[\sum_{t \geq 0} \gamma^{t} r_{t} \| \pi\right]$ with $s_{0} \sim p\left(s_{0}\right), a_{t} \sim \pi\left(\cdot \| s_{t}\right), s_{t+1} \sim p\left(\cdot \| s_{t}, a_{t}\right)$

Value Function

• (State) Value function is a prediction of the future reward

  • How much reward will I get from state s under policy $\pi$
  $$V^{\pi}(s)=\mathbb{E}\left[\sum_{t \geq 0} \gamma^{t} r_{t} \| s_{0}=s, \pi\right]$$

• (Action) Q-value function (quality) is a prediction of the future reward

  • from state s and action a, under policy $\pi$
  $$Q^{\pi}(s, a)=\mathbb{E}\left[\sum_{t \geq 0} \gamma^{t} r_{t} \| s_{0}=s, a_{0}=a, \pi\right]$$

• Optimal Q-value function is maximum value under optimal policy $\pi^*$ $Q^{*}(s, a)=\max _{\pi} Q^{\pi}(s, a)=Q^{\pi^{*}}(s, a) \Rightarrow \pi^{*}(s)=\underset{a}{\operatorname{argmax}} Q^{*}(s, a)$

Bellman Equation

Q-value function can be decomposed into a Bellman equation $Q^{\pi}(s, a)=\mathbb{E}_{s^{\prime}, a^{\prime}}\left[r+\gamma Q^{\pi}\left(s^{\prime}, a^{\prime}\right) \| s, a, \pi\right]$ Optimal Q-value function also decomposes into a Bellman equation $Q^{*}(s, a)=\mathbb{E}_{s^{\prime}}\left[r+\gamma \max _{a^{\prime}} Q^{*}\left(s^{\prime}, a^{\prime}\right) \| s, a\right]$

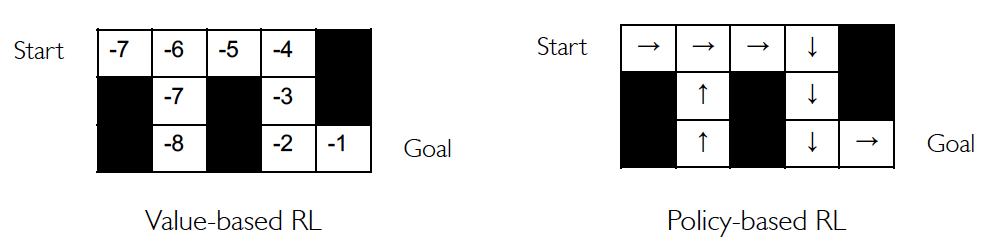
Value-based RL

• Estimate the optimal Q-value function $Q^{*}(s, a)$
• This is the maximum value achievable under any policy

Q-Learning(DQN)

Represent the Q-value function by Q-network with weights w $Q(s, a, w) \approx Q^{*}(s, a)$

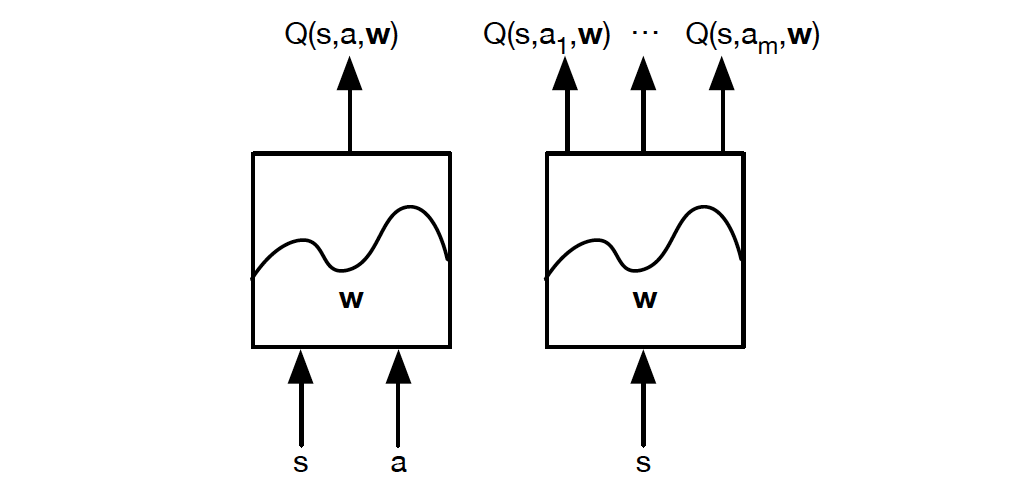
Lookup Table

Optimal Q-values should obey the Bellman equation $Q^{*}(s, a)=\mathbb{E}_{S^{\prime}}\left[r+\gamma \max _{a^{\prime}} Q^{*}\left(s^{\prime}, a^{\prime}\right) \| s, a\right]$ Treat the right-hand side $r+\gamma \max _{a^{\prime}} Q^{*}\left(s^{\prime}, a^{\prime}, w\right)$ as a target

Minimize MSE loss by SGD: $l=\left(r+\gamma \max _{a^{\prime}} Q^{*}\left(s^{\prime}, a^{\prime}, w\right)-Q(s, a, w)\right)^{2}$

• Converges to Q* using table lookup representation (Q-table) $Q_{t+1}(s_t, a_t)=Q_{t}\left(s_{t}, a_{t}\right)+\alpha\left(r_{t+1}+\gamma \max _{a} Q_{t}\left(s_{t+1}, a\right)-Q_{t}\left(s_{t}, a_{t}\right)\right)$

• But diverges using neural networks due to

  • Correlations between samples: to remove correlations, build dataset from agent’s own experience
  • Non-stationary targets: to deal with non-stationarity, target parameters w’ are held fixed

Improvements to DQN

• Double DQN
• Prioritized replay
• Dueling network

Policy-based RL

• Search directly for the optimal policy $\pi^{*}=\pi^{*}(a \| s)$
• This is the policy achieving maximum future reward

Policy Network

directly output the probability of actions $p\left(a_{t} \| s_{t}\right)$ without learning the Q-value function

• Guaranteed convergence to local minima
• High-dimensional (continuous) action spaces
• Stochastic policies (exploration/exploitation)

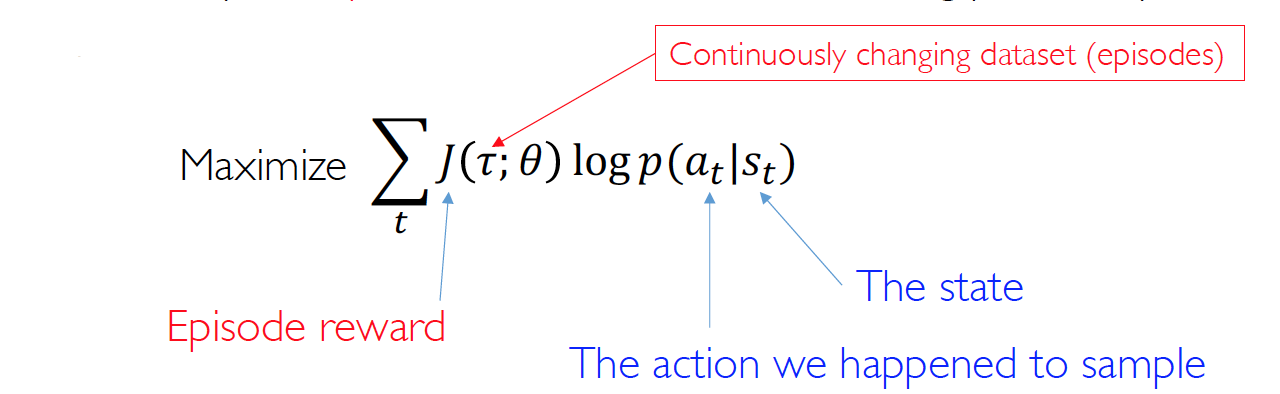
Policy Gradient(Reinforce)

policy gradients is exactly like supervised learning, except for:

• no correct label
  • use fake label: sample action from policy
• training when an episode is finished
• scaled by the episode reward
  • increase the log probability for actions that worked

Training protocol

For episode in range(max_episodes):

observation = env.reset()

While true (For each timestep) :

1. action = choose_action(observation)

2. observation_, reward, done = env.step(action)

3. store(observation, action, reward)

4. if done:

   ​ feed-forward policy network maximize $\sum_{t} J(\tau ; \theta) \log p\left(a_{t} \| s_{t}\right)$

   break

5. observation = observation_

Q-Learning vs. Policy Gradient

• Policy Gradient
  • very general but suffer from high variance so requires a lot of samples
  • Challenge: sample-efficiency
• Q-learning
  • Does not always work but when it works, usually more sample-efficient
  • Challenge: exploration
• Guarantees
  • Policy Gradient: Converges to a local minima of $J(\theta)$, often good enough
  • Q-learning: Zero guarantees since you are approximating the Bellman equation with a complicated function approximator