Lu Chen

Optimization

2019/07/10

Optimization

Objective Function

Loss function

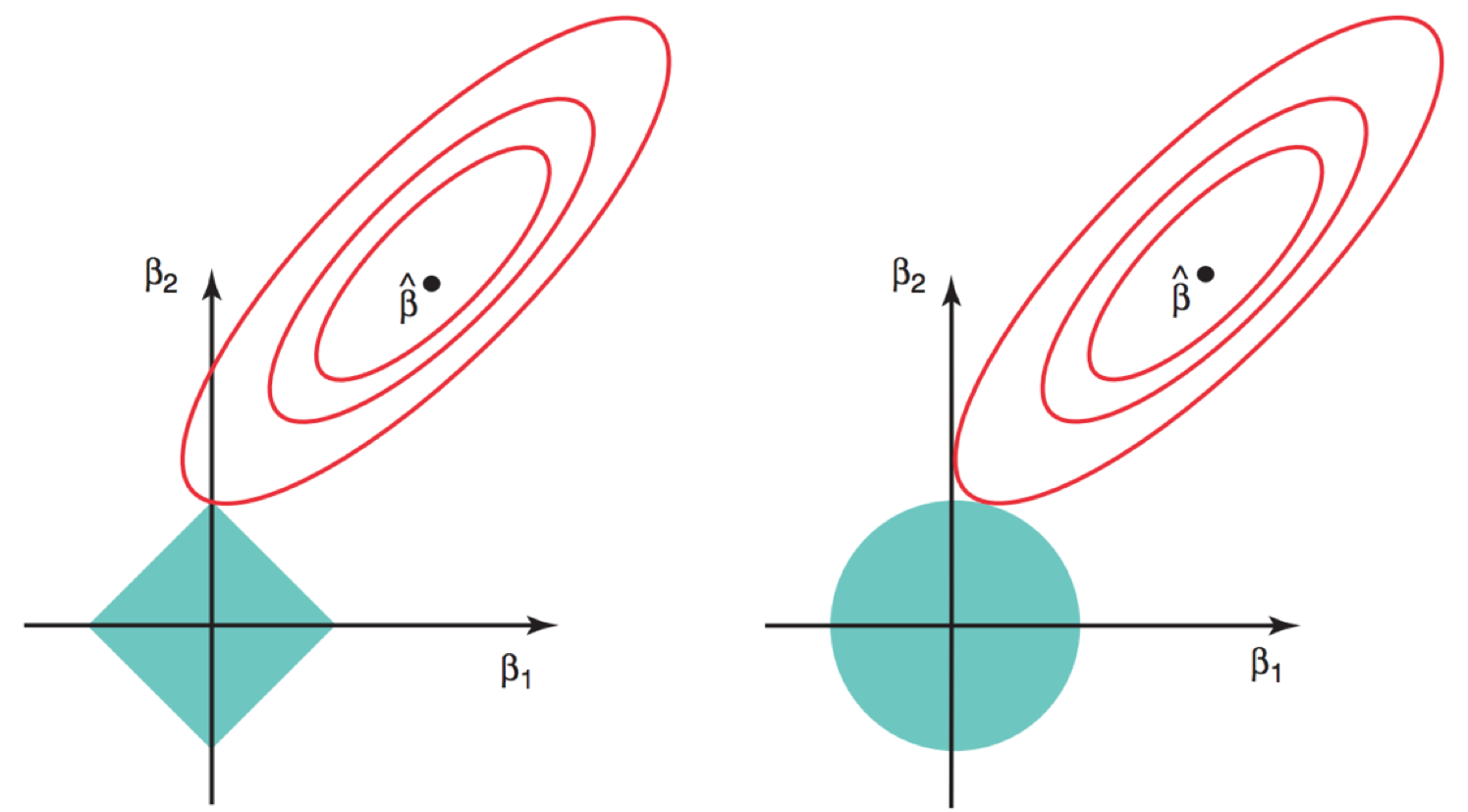
Regularization

image-20190719135201173

First-Order Method

Gradient（一阶梯度）

目标函数的一阶泰勒近似：

Gradient Descent(GD)

在 full batch 上计算梯度：

更新参数：

时间复杂度取决于数据量和参数维度，会在 zero gradient 的地方（鞍点）停止迭代

Convex Function

为了保证 GD 算法的收敛性，需要对目标函数做一些假设。

convex function:

f is convex if :

关键的性质：

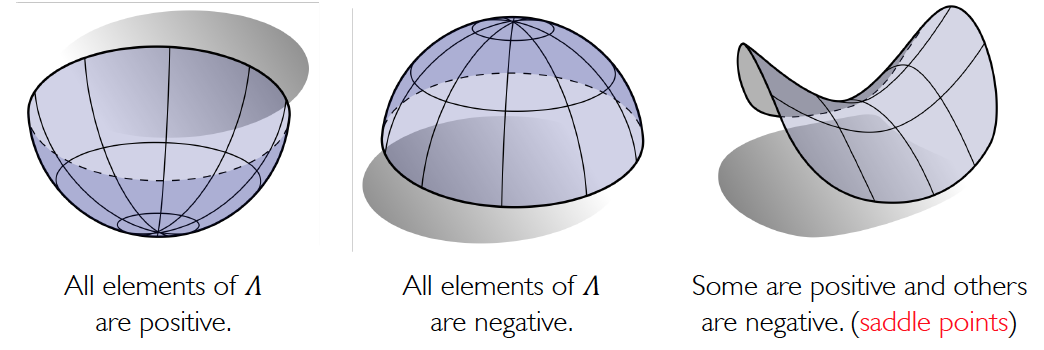
Second-Order Method

光一阶是不够的，在高维空间中，梯度为0的点叫critical points，有三种可能：

  1. maximum
  2. minimum
  3. saddle point

所以，当我们找到一个梯度为 0 的点，有可能不是最低点，所以这是优化过程中的一个难点。而且鞍点会经常出现。

Hessian（二阶梯度）

Hessian 矩阵可以表示 curvature(曲率) of function landscape 目标函数的二阶泰勒近似： 对 H 进行特征值分解：

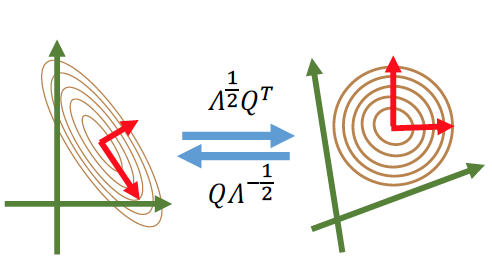
对角阵 决定了 the local shape of the landscape

Newton’s Method（牛顿法）

考虑在的小区域内二阶近似： 对求导，设为 0：是最优值 牛顿法的更新规则：

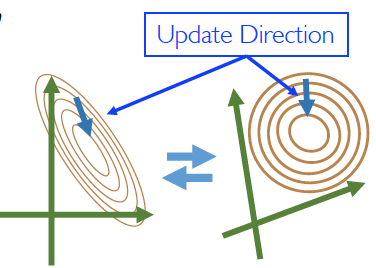
牛顿法的优点：比 GD 能够更快地收敛

缺点：计算 Hessian 矩阵的时间复杂度 O(d^2) 空间复杂度 O(d^3)， d 是参数维度，在大规模模型中是 impractical 的

Conjugate Gradient Descent(共轭梯度下降)

每一轮迭代：

  1. 计算
    1. 是使得和共轭（正交）：

  2. 计算

  3. 线性搜索：
    1. 是梯度能延伸的最大步长
  4. 更新参数：

共轭梯度下降是一阶方法，只需要计算不需要计算 H 和

使用了牛顿法的思想来调整梯度的方向，避免了在一个方向上的重复计算

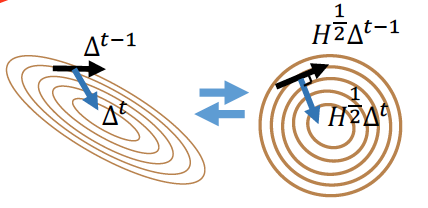
Quasi-Newton Method(类牛顿法)

为了避免每次要计算所以类牛顿法通过 incremental low-rank updates 近似

给定一个开始位置

  1. 计算类牛顿方向

  2. 更新下一个位置
  3. 计算

BFGS： where

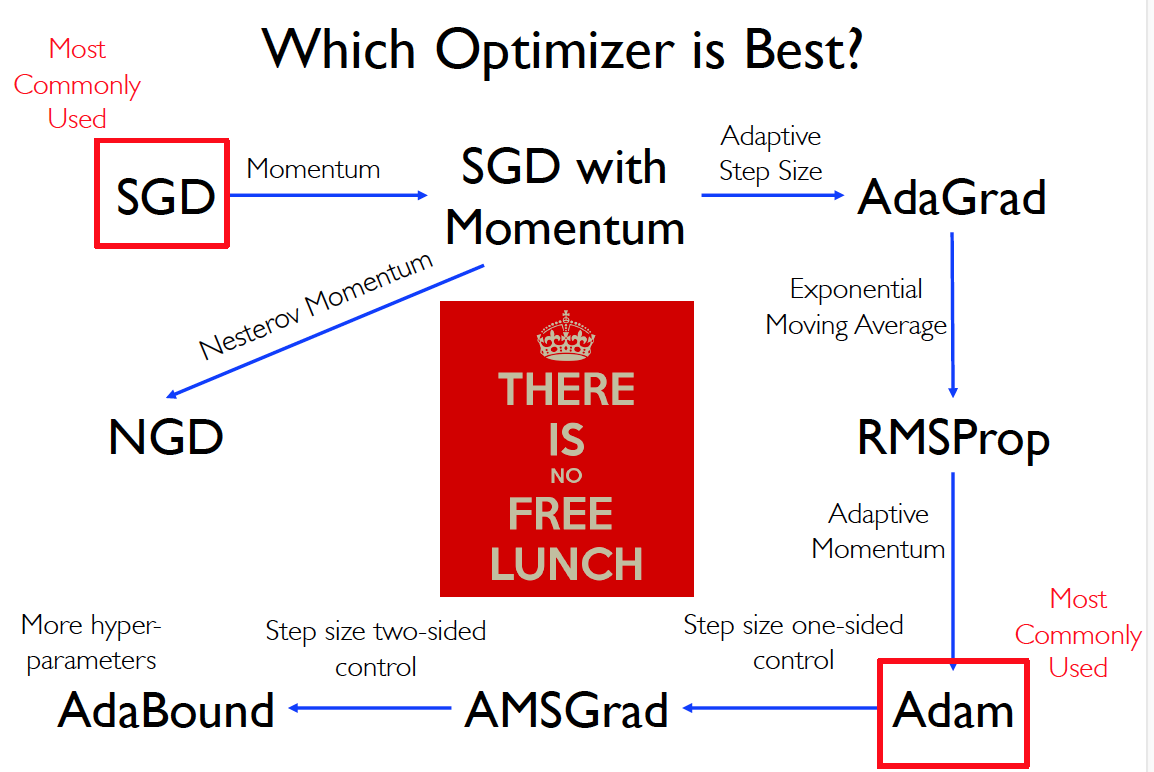
Optimization in DL

Stochastic Method

SGD

在一轮 iteration 中：

  1. 随机选择一个大小为 m 的 mini batch (在每个 epoch 中，都会 shuffle 数据集来避免 bias 偏差)
  2. 设置目标函数：
  3. 在 minibatch 上计算梯度：
  4. 用合适的学习率更新参数：

优点：

  • Stochasticity 可帮助逃离 saddle points

  • 比 full batch 的方法更快
  • 在 convex 条件下，理论收敛率：

缺点：

  • 因为梯度是在 minibatch 下计算出来的，所以梯度是 noisy 的，在不同 minibatch 梯度可能更改的很快
  • poor local minima 或者 saddle point 可能会导致 0 梯度，在高位空间中出现的概率更大
  • 目标函数有很高的 condition number:
    • ratio of largest to smallest singular value of Hessian

SGD with Momentum

和 SGD 唯一的差别是梯度计算：

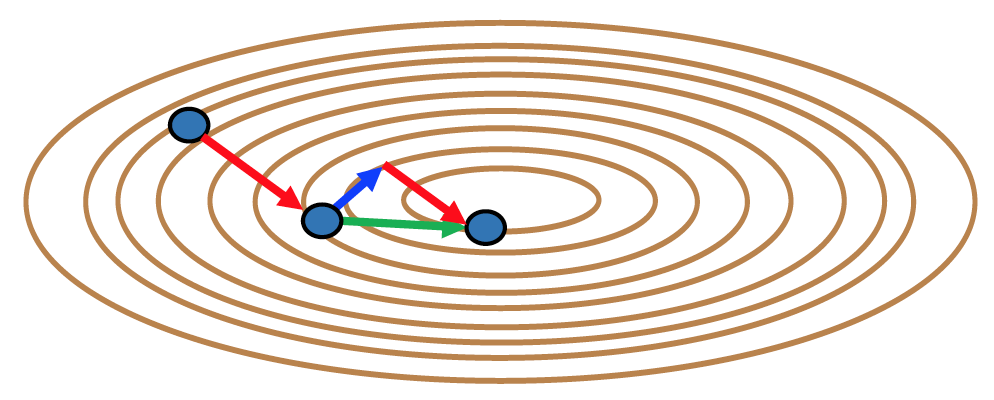
Nesterov Momentum

在加入 momentum 后计算梯度：保证梯度和 momentum 是同一个 time step。

加快了 momentum-based 的收敛速度

Adaptive Method

Adaptive Learning Rate: Learning Rate 的选择是对收敛质量非常重要的。

AdaGrad

  2. , 是一个数值很小的常数，防止除数为 0，

1，2，3 的维度和参数维度一样

随着迭代，adaptive learning rate 会衰减

RMSProp

Exponential Moving Average

加上了衰减系数在之前的梯度上：

和 Highway Network、LSTM 很像

RMSProp with Momentum

Adam

和 RMSProp with Momentum 相比，调整了第三步：

3.1

3.2

增加了 adaptive learning rate term for momentum

建议

完整版：

  2. : Normalize step to eliminate bias
  5. : Normalize step to eliminate bias

Leraning Rate Decay

在 SGD 中 learningrate 是超参数，为了使网络收敛的平稳快速，可以将 learning rate 设置为随着时间衰减，有两个衰减策略：

  1. Exponential decay strategy:
  2. 1/t decay strategy:

New Adaptive Method

在一些凸函数中，RMSProp 或者 Adam 可能会失败。这是 Exponential Moving Average 的问题：Adaptive learning rate 可能会随着时间 shrink

AMSGrad

改写 Adam 的第一步

1.1

1.2

所以 AMSGrad 保证了不会有 incresing step size

AdaBound

改写了 Adam 第2步

总结：

Post Directory