Lu Chen

Trie树（字典树）

2019/05/31

Trie树，又称：字典树，单词查找树，前缀树，顾名思义，字典树/单词查找树是用来查找单词的。利用字符串公共前缀降低搜索时间，速度为 O(k)，k 是输入的字符串长度。

为什么需要这样一种高级数据结构呢？

如果要从 n 个单词中查 m 个不同的单词，使用 map 可以很快查找出来。但是进一步的问题是如果要从 n 个单词中找到拥有某个前缀的单词。如果没有一个合适的存储结构来存放这些单词，随着单词数量的增多，每次查询都会耗时耗力。

Trie树是一种树形结构，是哈希树的变种(所以什么是哈希树？)

img

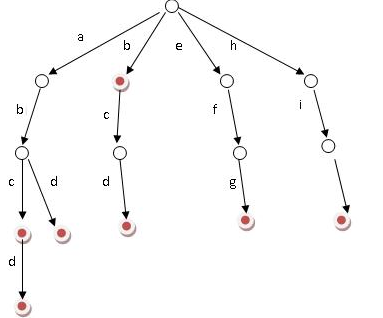
图中:

  1. 字典树的边表示字母
  2. 有相同前缀的单词共用前缀节点，那么每个节点最多有 26 个子节点
  3. 根节点不包括字符（这是方便插入和查找），除了根节点，其他每个节点都代表一个字符。
  4. 单词结束用一个特殊字符表示，在图中是红色节点
  5. 从根节点到某一节点的路径上经过的字符连接起来=该节点对应的字符串

应用

用于统计、排序、保存 大量的字符串

经常被搜索引擎系统用于文本词频统计

优点

利用字符串的公共前缀减少查询时间，可以最大限度地减少字符串比较，查询效率比哈希树高

基本操作

1. 插入 insert，插入一个单词

单词从左到右遍历，如果字母在当前树的位置出现了，就沿着字典树往下走，看单词下个字母。如果字母在树的当前位置的子节点下没有出现，则插入该字符。

设二维数组 trie[i][j] = k: 编号 i 的节点的第 j 个孩子是编号 k 的节点。编号 i，k 是指节点在整棵树中的位置编号，j 是指对于节点 i 的 第 j 个孩子。

j 的取值范围是 0-25，直接采用字母在字母表中的位置，但这样特别费空间，所有的节点都预留 26 个子节点的空间。如果要节约空间，应该是用到哪个就分哪个，不过这样查询的时候会费时一点，需要遍历一下所有子节点，判断是否存在某个字母。

对于一个关键词，从根开始，沿着单词的各个字母所对应的树中的节点分支向下走，直到单词遍历完，将最后的节点标记为红色，表示该单词已插入Trie树。

从根开始按照单词的字母顺序向下遍历Trie树，一旦发现某个节点标记不存在或者单词遍历完成而最后的节点未标记为红色，则表示该单词不存在，若最后的节点标记为红色，表示该单词存在。

Python实现

Trie 树节点：

class TrieNode(object):
    def __init__(self):
        self.child = {}
        self.flag = None # 1: 结束节点

Trie 树基本操作：

class Trie(object):
    def __init__(self):
        self.root = TrieNode()
                
    def add(self, words):
        curNode = self.root
        for word in words:
            if curNode.child.get(word) is None:
                nextNode = TrieNode()
                curNode.child[word] = nextNode
            curNode = curNode.child[word]
        curNode.flag = 1
        
    def search_exact(self, words):
      '''
      精确匹配，即输入与关键词完全匹配时返回True。例如 words = ‘child’，input = 'child’时返回True，input = ‘children’ 时返回False。
      '''
        curNode = self.root
        for word in words:
            if curNode.child.get(word) is None:
                return False
            else:
                curNode = curNode.child[word]
        return True if curNode.flag else False
            
    def search_fuzzy(self, sentence):
      '''
      模糊匹配，只要输入中包含关键词就返回True。例如 words = ‘child’，input = ‘child’ 或 ‘children’ 时都返回True。
      '''
        curNode = self.root
        for word in sentence:
            if curNode.child.get(word) is None:
                return False
            else:
                if curNode.child[word].flag == 1:
                    return True
                else:
                    curNode = curNode.child[word]
        return True

Post Directory